|
|
Derivation of magnetic field of wires |
|
Density pa =free electrons in a cubic meter: n/m^3 |
|
|
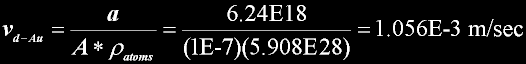
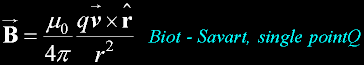
|
|
Magnetic field headed out of page at top, in blue, toward observer. |
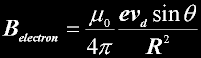
electron in motion |
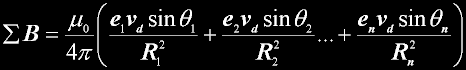
electrons in motion |
|
|
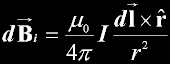
|
|
coulomb pairs |
|
|
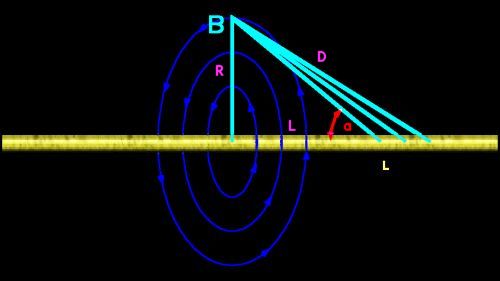
wire |


|

|
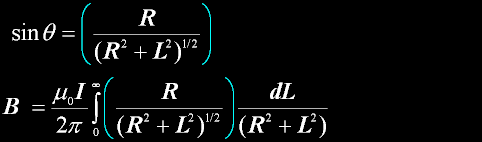
|
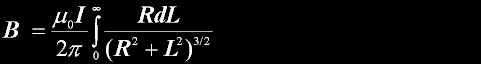
|
|
|
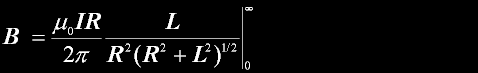
|
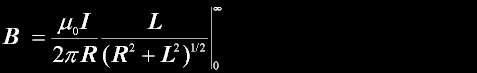
|

|
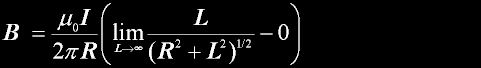
|
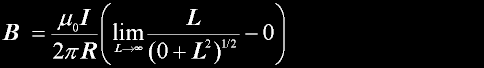
|

|

|

|
|
|
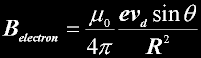
|
|