
|
Entropy |

|
|
Your riches are corrupted, and your garments are moth eaten.
Your gold and silver is cankered; and the rust of them shall be a witness against you, and shall eat your flesh as it were fire. Ye have heaped treasure together for the last days.
Behold, the hire of the labourers ...
James 5:2-4 |
| Heat |

|

|

|



|
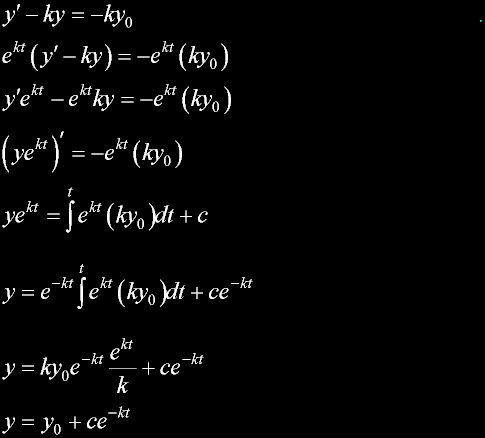
|

|
|
Exodus 23:20 |
|
|
|
|
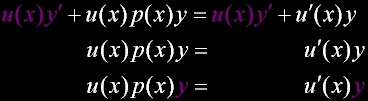
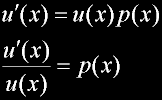
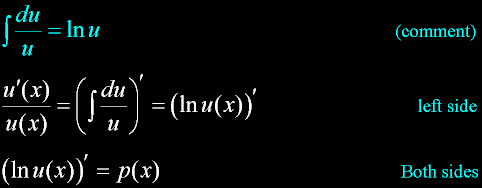
|
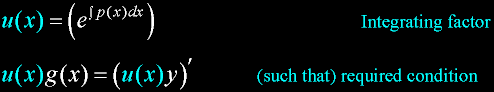
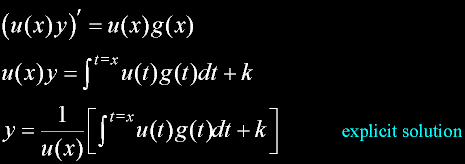
|
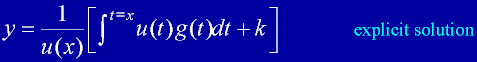
|
|
|



|
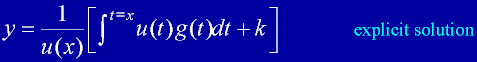
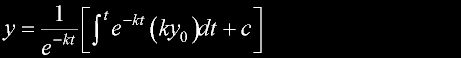
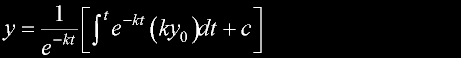
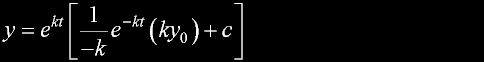


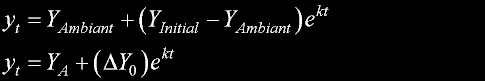
|


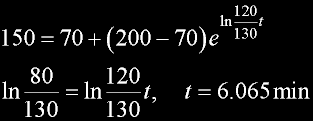
|
|
Matthew 6:20 |
|
|
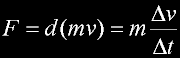
|
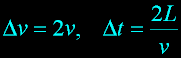
|
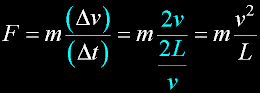
|

|
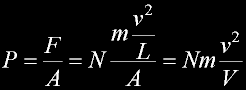
|

|
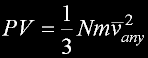
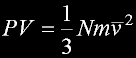
|
|
|
|
|
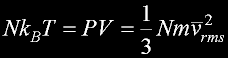
|
|
|
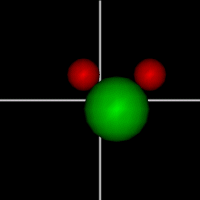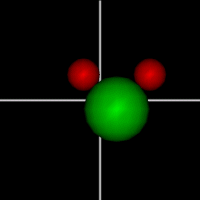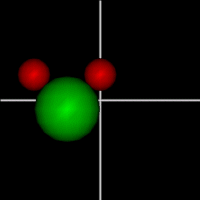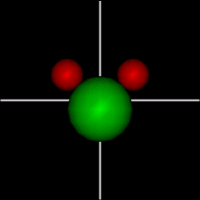 Translate x axis
Translate x axisTranslate y axis Translate z axis |
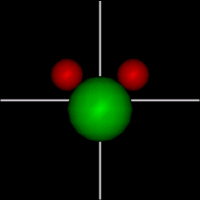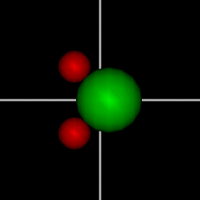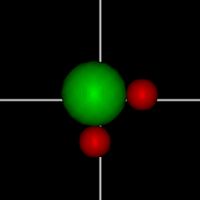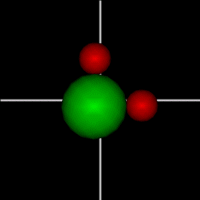 Rotate around x axis
Rotate around x axisRotate around y axis Rotate around z axis (Diatomic is only two. Monotonic noble gas is zero.) |
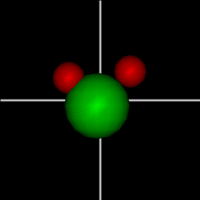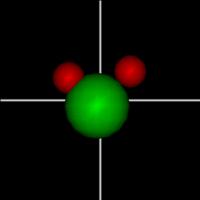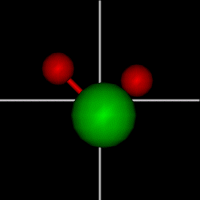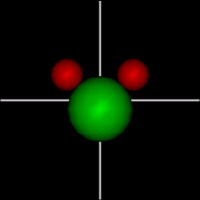 Vibration:
Vibration:Bond vibrate H1 Bond vibrate H2 |
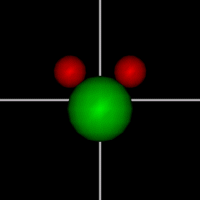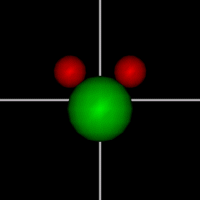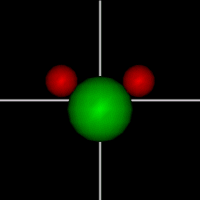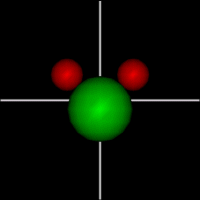 Vibration:
Vibration:Bond Angle vibration (active at room temperature for H2O) |

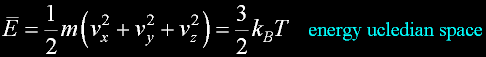


|

|
|
|
|
|
|

|


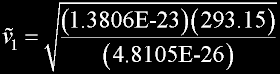



|
v(av) = 462.8 m/s v(rms) = 502.4 m/s v(prob)= 410.2 m/s (accurate)
|
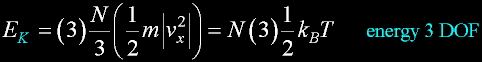
|
|
|

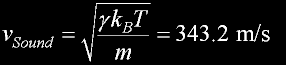
|
Specif Heat
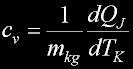
|
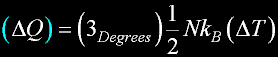
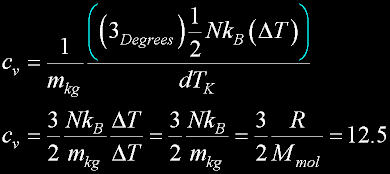
|
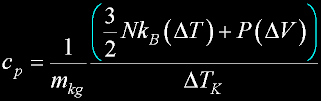
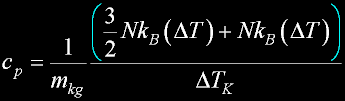
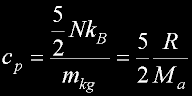
|
Second Law of thermodynamics:
Entropy dictates the flow of heat between two systems.
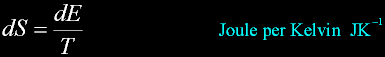
Heat energy involved in a transformation divided by the absolute temperature. 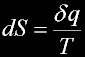
|