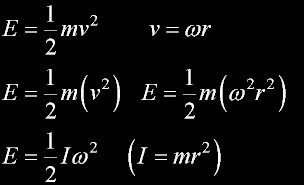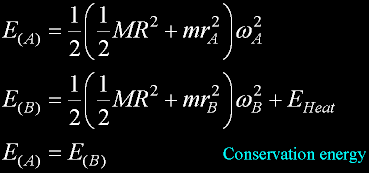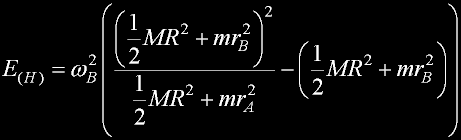
"In a garden, a weed is only a weed in the eye of the beholder."
If one defines heat energy as the energy of choice for entropy,
then here is an example of two stable newtonian states on a spinning disc.
A spinning disc is the closed world of a small car. The car is rotating on the disc and wishes to transverse
from point A to point B.
The spinning disc is naturally urging the car to move to a larger orbit.
Both points are stable as the car chooses to release braking force between points A and B, and to apply
full brakes at points A and B.
Or, if one car was a glob of clay, it could "jump" to point B and stick in an inelastic collision.
(This action is reminiscent of collisions of planetoids, and also subatomic quantum jumps.)
There are three laws at play here (as is always the case everywhere):
Conservation of momentum
Conservation of energy
Entropy
Entropy is produced through the simultaneous application of both conservation laws.
With such an application, Entropy can be accuratly calculated.
Angular momentum of the car...
Moment of inertia (I)
inertial energy of the car (E)
Conservation of inertial Momentum
Time symmetric; equally both directions
Conservation of Energy
Time symmetric; equally both directions
Solving the two sets of equations...
I hope that I have done this right. I dreamed up the problem with no way to check it.
But it looks right to me.
The necessary heat E(H) is positive.
There is no way it can be negative.
The heat is not reversable and represents entropy.
The temperature before movement compared to after movement is necessarily equal to one or greater.
(Delta T (Kelvin) is zero (no entropy) or greater (positive entropy)).
Position B is locked-in, and can not return to position A in this CLOSED system.
