Derivation of the gravitational constant

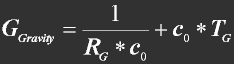
GRAVITY
Derivation of Gravity

Derivation of the gravitational constant, G

I am not a physicist. I am not even a scientist. I write computer programs. One program that I wrote compared different physical constants - one to another. I typed in the gravitational constant as measured for the 1999 value of Lou. The program flagged the value as equal to 1/50c. Almost exact! I can only guess at why this should be. If such a strange oddity were true, then the secret is in that number "50" and its relationship to the neutron and proton. Then, other data - newer data - was published for the gravitational constant. The new data slightly invalidated the relationship. In my opinion - "killed it"!

Oh well, truth is all that matters. In addition, what is more important - the dimensional units are totally wrong. I absolutely will not "cook", or pad, an equation. All that remained was to throw away the papers, and forget the time wasted. Just walk away. However, as a parting gesture: I should know exactly what is the difference between the values. Not that it really mattered; if it is wrong, it is wrong.

My first-term (old) value was (6.6712819E-11)
subtracted from the new 2006 composite measurement (6.67428E-11)
is a difference of 2.998096E-14. The mantissa is startling. To the accuracy of the measurement, it is the speed of light! Another oddity. Shamefully and uncontrollably, I then padded the equation with this new found oddity.

The result was three absolutely defined exact constants (c, 50, 1E-22) that arithmetically gave a value for G. Very strange; and with out any merit or reason.
R is the number "fifty". C is the speed of light. T is 1E-22.

"Engineered" Equation
This equation does not even qualify as an equation; It is more like a curious algorithm. Without proper dimensions, it is more of a relationship.
I will call this gravitational constant the "Engineered" constant, representing a curious and contrived arithmetical value.
However the value is accurate and quite intriguing.

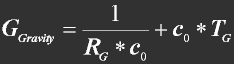
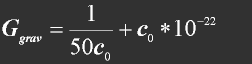
6.67259 (85)   1986 CODATA-86
6.673   (10)   1998 CODATA-98
6.6740   (7)   1997LANL-97 Bagley
6.6729   (5)   1998TRD-98 Karagioz
6.6709   (7)   2003HUST-99 Luo
6.674255(92)   2002Uwash-00 Markowitz
6.67559 (27)   2001BIPM-01Quinn
6.67422 (98)   2002Uwup-02 kleinvob 
6.67407 (22)   2002Uzur-02 schlamminger
6.67387 (27)   2003MSL-03 armstrong
6.6742  (10)   2002 CODATA-02

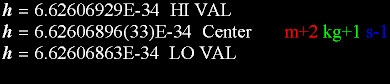
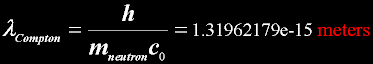
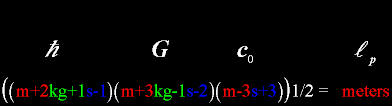
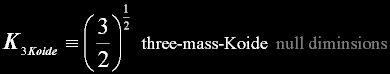
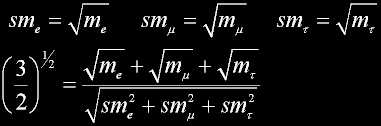
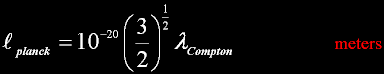
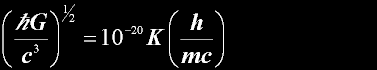
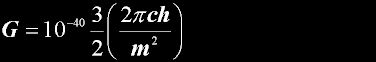
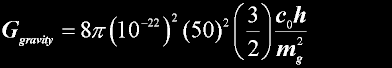
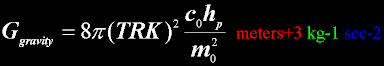
Condensed and evaluated Empirical gravitational constant from data...

Without Units, this thing means NOTHING! Playing with the computer and just looking at "numbers" is no way to do business. So I decided to switch tactics and look for "units".
RULERMAR.GIF, 1 kB

Gravitational constant derivation (with real dimensions).

The first equation that I reference: the Compton wavelength.

h is empirically known...
c is defined...

For example: the neutron wavelength.
And I have chosen the neutron for a reason. Regardless of the specific mass, we have a relationship between wavelength and mass.

RULERMAR.GIF, 1 kB

The second equation that I reference: the Planck length, derived from "compatible units".
Planck-length is derived from compatible units.
This is very important: There is NO information about specific coefficients. This fact gives me freedom to let the computer "choose" them.

Of course other equations for G are possible when using dimensional analysis. And all with no guaranties of applicability. And all with no information about coefficients and constants.

When restricted to these three variables: Mass, Gravitational Constant, Planck Length, and Velocity of Light, this is a REASONABLE equation - based solely on units.

RULERMAR.GIF, 1 kB

What is needed is a third equation...

I reasoned that I needed a SINGLE mass unit to put into the above equation. Most of the mass of substances can be represented by the nucleus with its neutrons, or Protons-plus-electrons. This is true whether measurements have been made using the iron and nickel of the earths core, platinum-iridium in experiments, or brass balls. A "nuetron-mass-unit" is just as easy and comparable as the atomic mass unit based on carbon-12.

The mass of the neutron was substituted into the planck equation.
I stood back and let the computer run with it.

My computer handed me yet another oddity: a beautiful relationship between the two equations.
There it was on the computer screen. In total disbelief, I double checked the computer. It seems to be correct.

I therefore assert this equation:
I will call it the Planck-Compton-length relationship (and it is only true for the neutron). What is the computer showing me now? I seem to be the first to see it. (Not counting the before mentioned computer)

I extracted the constant from the Koide equation, which I will call the Three-mass-Koide constant.

For my computer to find this relationship I had to tell it previously about a little known constant. Which was set aside as a curious oddity: the Koide equation. This relates the masses of the leptons: Electron, Muon, and Tauon.

Substituting the constant K - just as my computer had done.
And it turns out to be correct.

Combining the two equations...
Solving for G...

Dividing up the dimensionless factors a little differently...
Gravitational constant using the two terms of the Engineered equation.

I will call it the "Neutron-G equation", and it is for only ONE mass. Although the Koide came from Leptons, we are dealing with hadrons. It still could refer to a real mass like the neutron. Why this is so, I do not know.
According to the equivalent principle, this equation should not exist: There is no difference between inertial mass and gravitational mass. Gravity should not depend on an arbitrary mass. UNLESS! - The neutron has a planck length and is composed of three "kodie-like" particles. At least the units are correct now, however the computer still has a free hand with the coefficients.

RULERMAR.GIF, 1 kB

Now, to take the equation out for a spin...

Here is a formula value for a virtual proton-plus-electron. (1.672621637E-27 kg) + (9.10938215E-31 kg)

Here is the value for pure hydrogen atom: one proton, zero neutrons. 1.007825u. This is a specific nuclide and does exist as a stable natural "unit".

This value is close to free fall measurements like
G = 6.6873E-11 of Schwarz1998; using tungsten.

The original premise was that it had to be a hadron. Therefore, the last two examples are not applicable.
Here is the formula value of the formula Gravitational constant for the neutron.

Which is close to the G=6.67387(0.00027)E-11 Armstrong2003

The last accepted empirical value of Codata - 2006.

So what does this mean? I do not know.
My computer just loves dimensional analysis: it gives it vast liberties with coefficients. Countless permutations! Perhaps I should have walked away when I had the chance. But my computer has this uncontrollable compulsion to play with numbers. I am out of breath and tired of chasing it. It is brutally efficient at what it does.

C.A.Pennock
RULERBOW