Derivation of Maclaurin expansion of Lorentz factor Derivation of Lorentz Factor>

First, I wanted to expand the Lorentz...
Ideally one would want to expand near the speed of light v

You can work in terms of the inverse or normal. I will derive in normal. Or when you are done, you can invert the individual iterated terms. That is easy.

Derivatives of functions of v are not defined at zero.



I am first going to substitute a specific value, far from zero.
I am not really expecting much.
The value that I am going to choose is a velocity of the square root of two, of the velocity of light.
With this value, the square of beta represents one half of energy. And also, gamma represents an exact value of the square root of two - which is accurately known.




The first evaluation is with the computer simply evaluating the direct expression, in double precision. And it also agrees with the square root of two as found in tables (to 15 places). So this is "gospel"

Here are the iterated Laclaurin values.
Terrible approximations!
So, at least for this "far away" value, this kind of accuracy is useless.




Now for a close-in value to zero.
Great approximation! No surprise. That is where I expanded from. x=0.




Another value...
The same as a trig identity...

The value can be double checked
because the secant of .1 is also 1.00502091840046 to 15 places.



I had an alterior motive in looking at the Lorentz Factor: I wanted to also look at my computer.
My computer seems to have about 15 digits of accuracy in double precision. Double precision works with 18 native mantissa digits, outputting 15. Accuracy may start out with 15 digits; This is the most that can be expected! Accuracy immediately begins to suffer as soon as manipulations are started. It is sort of like damage to DNA strands. The more manipulations, the greater the damage, and the greater the loss of accuracy.

Also, one variable may be compromised in accuracy, and affect the accuracy of all the rest and the end solution. It is sort of like the weakest link thing. Order of operations can hurt the accuracy of any member, as head room is lost and rounding errors creep in.

But enough of playing around with computer accuracy. Got to get back to the original physics problem.


The above is a useless expansion. I must find a way to expand near v=c.


First, I'll investigate making velocity into a complex variable. There is no evidence of this, but I will assume speed is a complex quantity. I will map the imaginary component of speed to the y axis of a conventional real xy plane. And then under recursive manipulation, turn the display into a fractal pattern.


Here is the code engine, the part that does the critical work. The numbers on the left are line numbers of the code. The hyphens indicate a "comment" in the code and are not executed. The code is Visual Studio 2019.

Each new XR and YR are re inserted into the Velocity of the Lorentz Contraction. Around and Around. Each time the iteration is counted and analyzed. It is a measure of "roughness" or ease of convergence. To square XR, XR is multiplied by itself, because this is faster to compute than taking the square. Also, I have drawn in explicitly c as squared just for clairity. But then, not in this view, I changed c back to "1". Only because the program executes faster.

Sometimes I temporarily remove the square root, as I have shown here. It changes the scale of the picture. But there is a reason: the program language can not process the square root of a negative number, unless I step in with additional code. The omission is in the spirit of brevity because, at this point, these are only pretty pictures, and I have no idea what it all means. After all, who ever heard of speed as two dimensional, or velocity as four? But then again, you could safely argue that every number is a complex number.
So, who knows? I am just scribbling with my crayons...


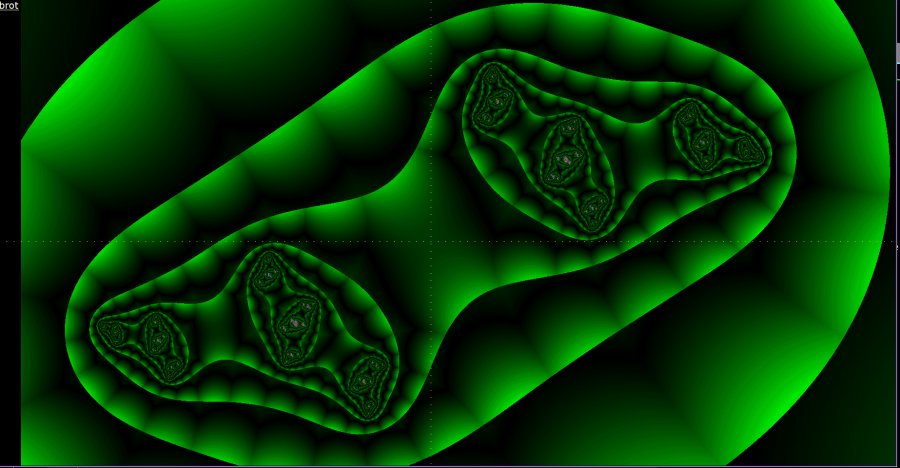This plot is of the Inverse Lorentz lamda=(1-v^2)^.5 without the square root. There are significant attractor poles in quadrant 1 and 3. There is a three-cluster pattern that keeps repeating forever.


There is an infinite way to display stuff. This is still the inverse Lorentz. I do not know what it means. Just pretty pictures at this point. The "waves" in blue are an artifact of the displaying, and have nothing to do with the mathematics. I was taking large values, for example 3000, and subtracting off 255 until the value falls below 255. Each new "255 set" produces a wave that is only indicative of the display mechanism.



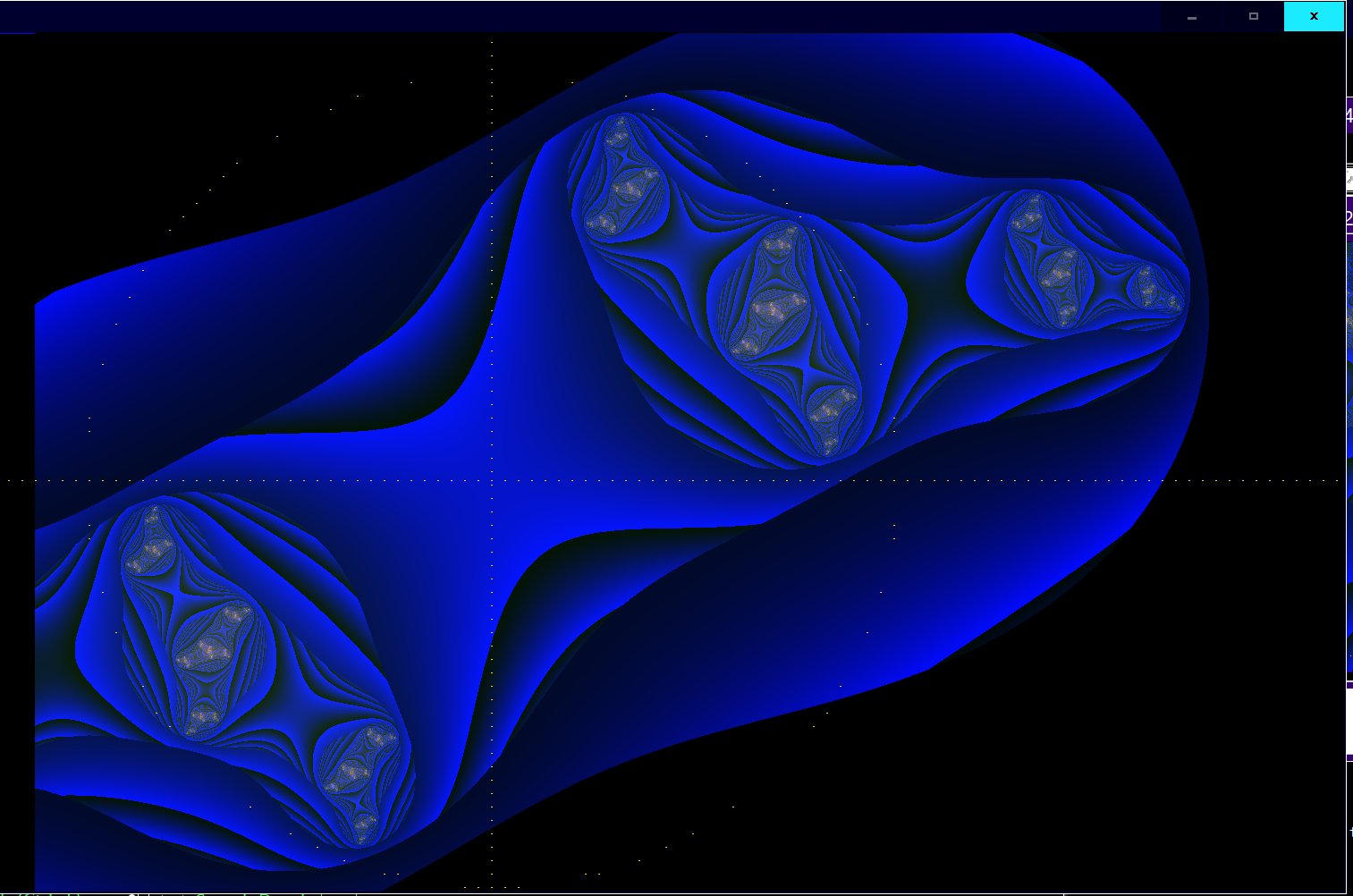
There are so many ways to display the same stuff. You can choose many criteria for the iterations to converge too. And three color choices too. All pretty.

There are no equations possible that can describe fractal designs. No equations have ever been written that can handle recursive iterations. Fractals are ordered chaos. All that is around us can only be simulated by a computer. But the magnitude of the computer would demand that the computer would be the very reality that we see around us. There are no individuals in fractals and chaos, only well ordered classes that will yeld fruit that, in the present, have not yet materialized. The future of a drop of rain, in the present, literaily exists equally in many worlds at the same time. Materialization is a wonderful phenomenon played out in a Natural computer called Reality.





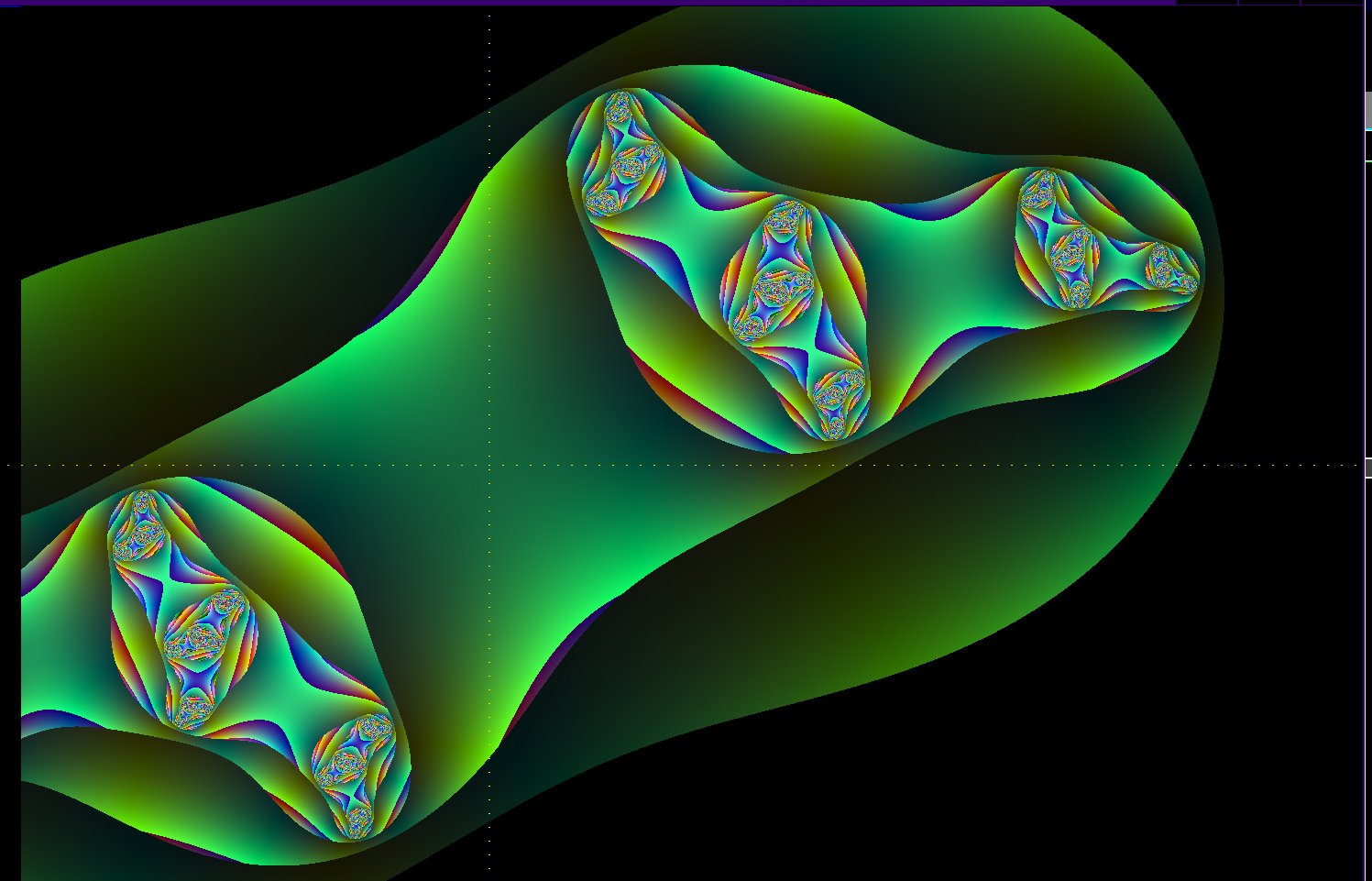
Criteria is for the squares of the real and imag components of v{n+1} to be greater than 1. This detail is more realistic and informative. Display Gain of 1


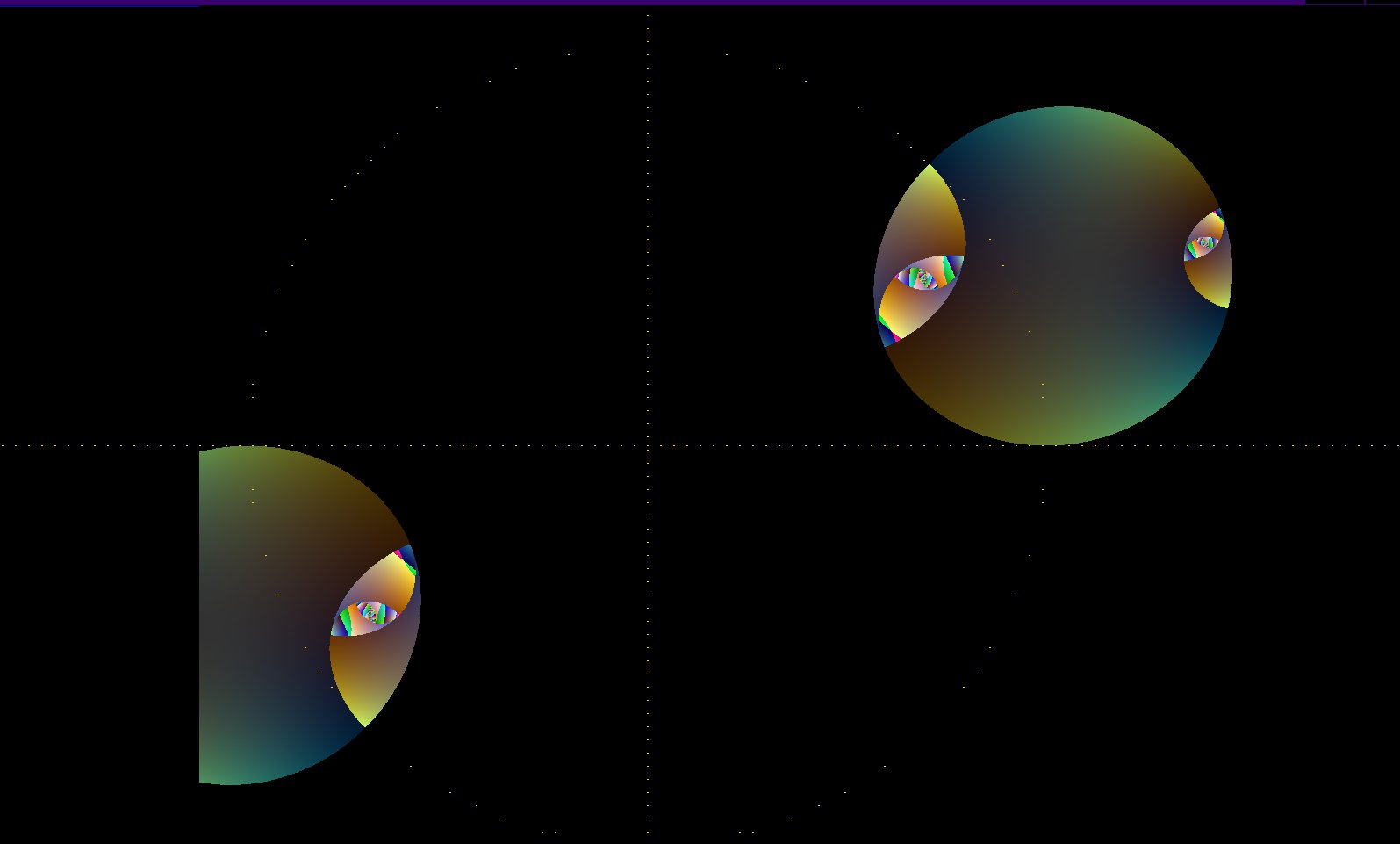Criteria is for the sum of the squares of the real and imag components of v{n+1} to be greater than 1. This detail has two high of gain. It is 5. Looks too cartoonish.


Reducing the gain to 2 gives a better display.
The circle marker is c the speed of light.
Looks like triple flower pedals, in a visual way, in quadrants one and three.
And in the above pictures with the criteria too high at 4, the smooth detail was destroyed. It is a fine balance.
But the "triple" character is still identifiable. Also now, the speed of light only on the real axis is unremarkable, as it should be.



Here is a zoom in on one of the pedals. Seems to repeat as a fractal. It has that fractal look.


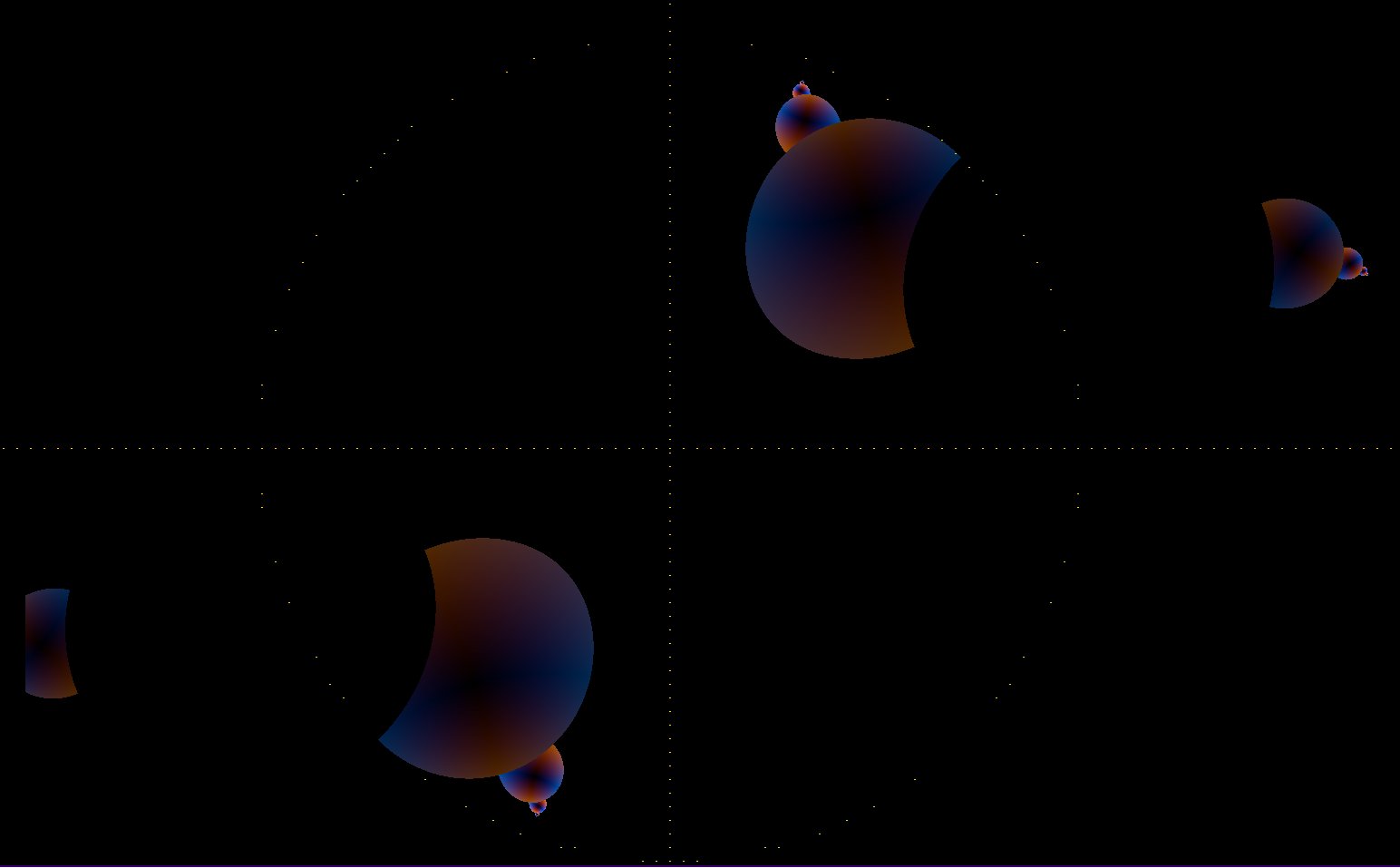This is with the Criteria set to less than 1.
Criteria is for the sum of the squares of the real and imag components of v{n+1} to be less than 1.
There are so many ways to display this stuff... Everything is the same, except the criteria is for less than 1. Results are different. With some black holes replacing other plots.
With some extra balls thrown in. Interesting balls. Pretty balls.



This is with the Criteria set to less than a half.



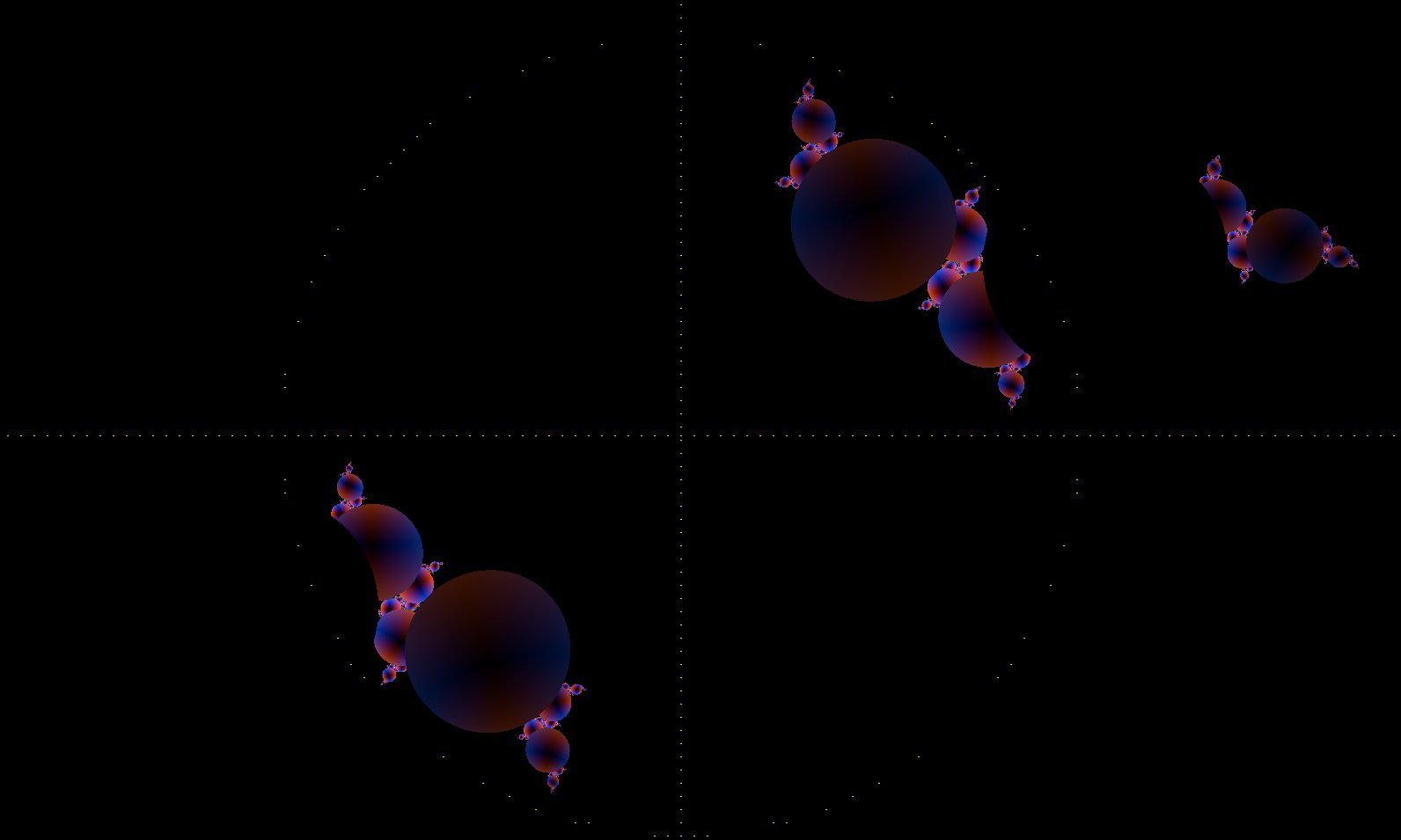Less than half





I am going to derive the Lorentz Transformation. Not a formal proof, but a valid algebraic solution. First I set the sceen, and referense Michelson and Morley silvered mirrors forming two orthoganal paths. The observation was that the travel times of the two light beems are always invariant of the speed and direction of the apparatus. Nowdays, with lasers, this effect is verified with high precision. You can not determine your travel in empty space by measuring length of rulers or timeing light beems.

I have found that you do not even need the transverse path to calculate the Lorentz, only to determine if an Either exists. And in that regard, Michelson and Morley were succesful; howbeit a bittersweet experience.

To calculate the Lorentz you only need one physical set of paths: The two parts of the path established by the silvered mirrors; two longitudinal portions, one forward and one return backwards. You do not need the transverse paths at all. One set of physical paths, the longitudinals, but two very different assumptions about those paths. To calculate the Lorentz you need to compare two assumptions: one assumption is that the frame, in this case the Earth, is stationary. This will be our reference assumption. Obviously, this eliminates problems, and gives the correct answer: the speed of the Earth is invariant, or zero. The other assumption is the opposite, and is that the Earth is moving, and naturally carries a given rudimentary assumption that is quite persistent and intuitive; And that is that you can algebraically add and subtract velocities. Every school kid knows this. ...And a third thing, already proved by Michelson and Morley. Very important! That one of the assumptions is wrong.

That is OK. If one of the results is wrong, a correction factor can be applied to make it right. You can make the observation fit. In fact, that is the mechanism that I will use to find the Lorentz.

So, to begin...

Any school kid can find the time for each portion of the path, T{1} and T{2}. After all, it is so apparent. It is a trivial matter to add or subtract the times. Knowing what we know today, I will call this path the "Relativistic" path, even though at this point there is nothing relativistic about it. The other assumption, which fits the data, about the physical path is the opposite: that there is no motion. It is the reference assumption. It has a simple time of 2D/c. I call this time T{o}, with zero velocity, or Original frame at rest. If there is any frame that we humans can call a reference, then this is it. Actually, the correct interpretation is that the speed is invariant, always giving the same result of a frame at rest. Obviously, we have to reconcile these two shockingly different results with a Correction factor. At this point, we do not know the mechanism. We will simply fix the problem. Agreement is paramount, and agreement to what Michelson and Morley found are the facts of the experiment. It will temporarily be fixed with a hammer and brute force, with no incite.

But there are two variables that the Correction factor can be applied two:
One is Time, and the other is Distance.
At this point we do not know which is changing, or both. All we know is that something is damn well changing! It is a fact of observation of not only Michelson and Morley , but of every human on this planet.
In this case I will start by, arbitrarily, appling it to Time. Ask for forgiveness later... It is simple algebra to work out the times. And after the correction factor is applied, the results are finally the same. Problem fixed. Importantly, the problem is completely and totally fixed. It is a simple fix, but a blind fact that works.

But we are nieve and operating in the dark because there is another way to completely fix the problem too.
And that is by applying a correction factor to D the Distance. Perhaps something is mucking with the distance. And when we do. Well, there it is... The same factor but the reciprocal. It totally fixes the problem too. It is a blind fact. Another brute force fix.

In either case, the math is down right bullet proof. But that is not the right answer! It is correct for the data, but it is not the Lorentz. All of the above seems right:
The Time is changing in the right direction. Time is dilating as v is approaching c, the velocity of light. That is correct. The distance is also changing in the correct direction. It is compressing in the direction of motion. That is correct. But neither alone seems to be the correct answer.

By observing that BOTH have the correct BEHAVIOR, we could be on the correct path, and indeed with some insight, we have stumbled unto the right course to get the answer: BOTH distance AND time are changing TOGETHER. It is not a case of one or the other. How else could they change? Time and Distance are linearly and proportionally linked. In fact, they form v, v=d/t. What happens to one happens to the other. So, I give both time and distance each their own independent Factor lambda. Then the Lorentz Factor is easily derived from the "over-all" Factor F{T,D}. QED


There is another way to do this. And it is totally intuitive, with no apparatus required.


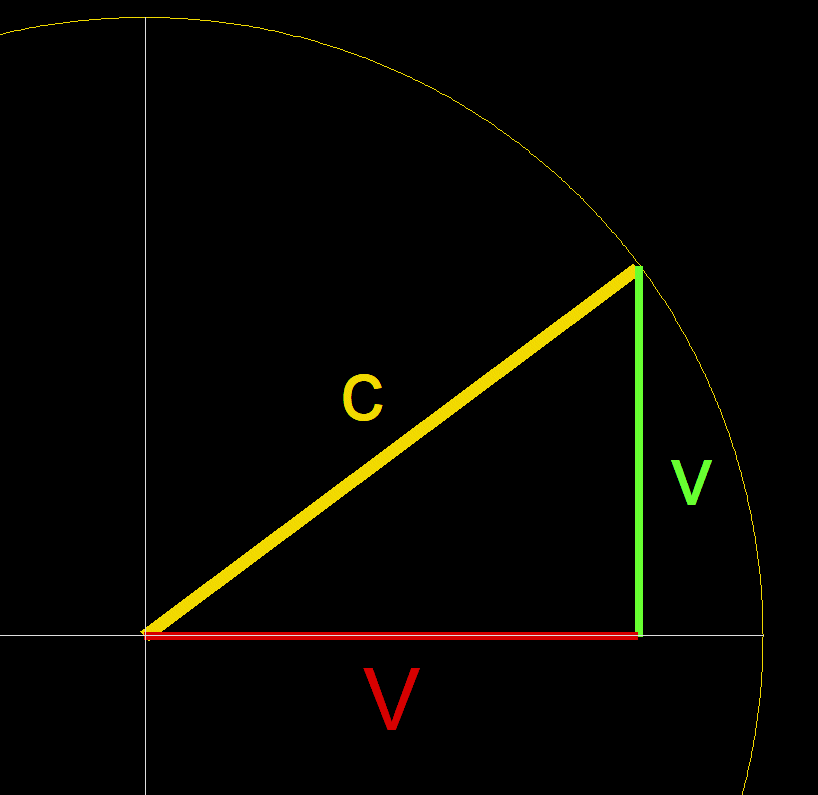I am going to draw this as a circle, but it is not about velocity. Here is a circle expressing the notion that I held in the 8th grade: That the speed of light is a constant. I choose a circle. And more specifically, to my diagram, that all components to that speed, together, can not exceed the magical value c, the hypotenuse. Everything is speed. The horizontal axis is speed, as well as the vertical axis. No where is velocity. Just pure speed.

The horizontal axis is the net result of internal speeds of constituent particles. Every object is made up of subatomic particles; quarks, neutrons, protons, electrons, atoms, etc. In High School I had little knowledge of these, so I called them "polytons". No one could make up such a generic stupid term. I threw out the notion of what you called them. I did not give a damn. It made no difference. So Instantly, I was known to be crazy.

The vertical axis is the Speed of an object: the "outer" polyton. Usually something big, like a car or planet. The vertical axis is the speed being measured by an observer. Nowhere do I invoke relativity. That is the beauty of my idea in youth, and I got the same results as relativity. But much more simply. I was quite conscious and exited about this. But better discretion amongst my friends limited my High School image to only "odd".

I was not able in a paper submitted in High School to adequately describe this, nor of my Special Entropy, which is related. But "Speed" is only germane here. The speed measured by the vertical axis is highly dependent on the properties of the horizontal axis: The properties build and constitute material rulers, and material clocks. That is physically what they are, and that is what they are made of. They are made of stuff in the horizontal axis. It is matter that we exist in, with all its internal speedy things.

The vertical is pure conjecture, which is a measurement by a mind. However, the precision is high and is quite specific. It is the determined speed of an object.

The part that I failed to do in high school is square the sides. Sadly, it is like I did not know about Pythagoras. I only held to a verbal notion that the sum of all speed of light could not be exceeded in a linear direction, and a feeling of how internal "polytons" were affected. I have to stop using that term.

From the diagram, the observer's real velocity, or velocity measured, is sqrt C2-V2. You can also write this as sprt 1-V2/c2, which is almost the Lorentz factor. And it is dependent on the ruler,V. From the diagram, as an observer increases speed, the internal velocities, V, decrease. C, of course, stays the same somewhere on the circle. Just geometry.

So, internal velocities, on the horizontal axis decrease. No matter how a clock is made, when internal velocities decrease time-rate inflates, takes longer between ticks. The particles are moving slower. An analogy would be a rotating electron clock. The period slows, and time between ticks increase. ...Just physics and Counting.

Also distances shrink in the physical media of the horizontal axis, as internal speeds slow. An analogy would be with Pressure: a balloon of air molecules shrinks in size when the temperature inside decreases, as microscopically, inside molecular speeds decrease. A fundamental measurement of distance can be seen on the surface of a balloon due to unseen internal speeds.


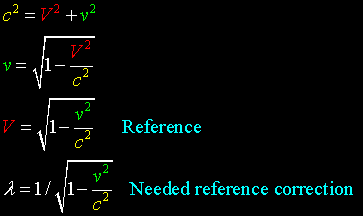Now getting back to the vertical axis. Stubbornly, the observer will have none of this: His measured number is v. Not sprt 1-V2/c2. He saw it with his eyes, which are made of the same internal stuff, and he measured it with the horizontal axis stuff, and it seems quite accurate and concrete. But it is not so, as the diagram shows. An invisible demon is mucking with his ruler. By how much? Naturally, the ruler, the standard, has changed, indicated by the diagram. So a correction factor needs to be applied to his velocity to account for his new reference. It is: 1/sprt 1-v2/c2, which is the Lorentz factor. Of course the observer can keep his v, if he blissfully stays in his frame.

This is all from the notion that "you can not go faster than the speed of light". So simple. So real. Who needs Einstein?

I like this solution, for it gives the reason. My previous solution gave no reason. It simply gave a correction factor, regardless of the cause. It presented only a physical measurement. But this solution is different. I love it because it gives validation to the years when I was not understood. It gives a theory, and understanding. And it brings the emotional heart and soul back into the equations. I love to live there.


Can I make a valid jump to Energy? All the "velocities" are squared. I can write an Energy equation:


Let c^2 represent Energy that is predefined. The core value is exact and never changes. Define the essence in terms of Gravity, c, and h. This is the Absolute Total Energy

Let V^2 represent Energy that is observed. Both kinetic and potential, in all forms known. This is Common Energy of experience and measurement.


Let v^2 represent Energy that is hidden or Internal. And it constitutes a standard for all forms of rulers, and all forms of clocks. This Energy is a factor of devaluation and inflation.





This plot is only a mathematical construct. Nothing to do with the Lorentz. This plot is of all points in the xy plane P(x,y) being represented as complex point P(x,i), The complex points are then squared, and the resulting components (x,i) are remapped to real values as (x,y). Each x component is colored, and each y component colored. X components in red as xc, and y components in blue as yc. Colored components (xc, yc) are placed back in original location of P(x,y) in the display plane.

To the right is saturation of both colors of red and blue. It is an artifact of the display: When any color exceeds a value of 255, it is reduced modulo 255, and starts over. The result is "banding". But I wrote the program that way, and as long as I know what is going on, then I like it. This method can extend, or reuse, the set color range of 0 to 255, for any of the three colors. If I do not care about resolution, I use a different techneque: I simple represent a color number by a larger proportion that yelds a more gradual shading to cover a larger range. But the modulo method gives a higher resolution.




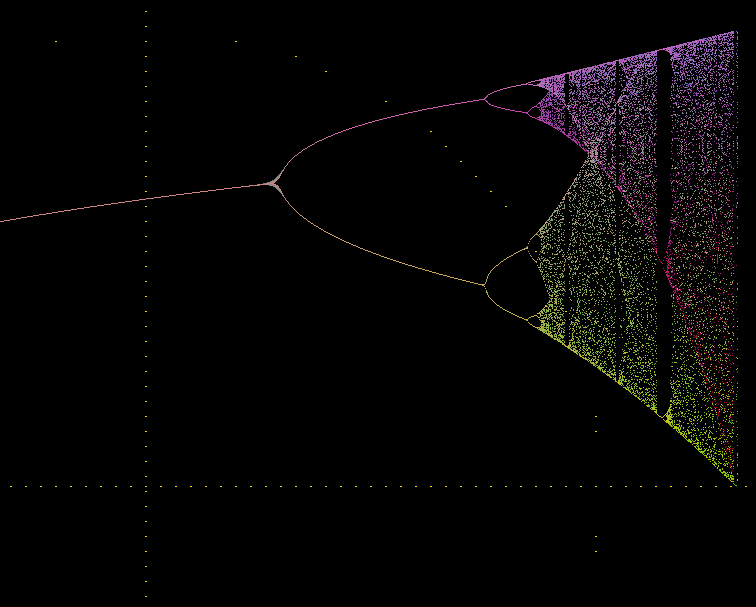A related fractal, using only real numbers.
x{n+1} = rx{n} (1-x{n})
x{n+1}/r = x-x^2
with the added x term, complex numbers are not convenient.
Fascinating not to have to work with functions that yeld one value. This fractal yelds all kinds of simultaneous values out past 3.


Already knowing how to square a complex number, and knowing what it looks like, I am prepared to plot the Lorentz which uses a square term. And more importantly that square term can be velocity as a complex number.

The Lorentz that I am using is the inverse, or the one used for distance. lam=(1-v^2)^.5 You can see as real values approach c, represented by the dotted circle, not that the limit will be a circle, the real values in red go to zero. That makes sense. And that is what the Lorentz says; distance compresses and goes to zero. In this diagram, Distances start up again as the velocity of light is exceeded, due to squaring negative numbers and absolute value treatments, an artifact of the math and program, and not the physics. AT least, I assume it is the math. Math seems to intrinsically determine physics somehow. Nowadays, Physics has no sovranty around here.

But in the imaginary vertical direction there is NO limit to the velocity of light! Does this have something to do with distance coupling as in Entanglement? I see no regard for any kind of a limit. This indicates, that with the right equations, the speed of light could be exceeded. Or the converse, the Lorentz needs to be re written to include imaginary numbers.

There seems to be more structure to the mandelbrot. One display is a mandelbrot with one variable and one operation, and the other is a function with a variable. Both these displays are in three dimensions, but are displayed in a two dimension xy display. The mandelbrot has the x variable in the x dimension, the imaginary in the y dimension, and the iterations in the color dimension. The functions have the x variable in the x dimension and the imaginary in the y dimension, and the dependent variable in the color dimension.

How drastic the difference in the two types of display! The mandelbrots are so rich. I must concede that the mandelbrots have an infinite number of criteria. And thus can paint some interesting patterns. None are not directly computable. On the other hand, the function oF a variable, by definition, has only one result. Unfortunately, it could be boring. A rifle has high precision, but one shot. The shotgun has a lot of possibilities, but vague meaning. When I say vague, I mean not computable. In fact, I would say, that even if you had a computer the size of the earth, and in fact, was the earth itself, you could not repeat anything. You could not simulate anything. Talk about uncertain...

And guess which one defines us, and everything around us; it is the fractals. The world of the fractals. No wonder life is so complicated. Gotta go outside and work in the yard...


This is kinda related to fractals...
I have written before of the fate of advanced civilizations. And of how efforts, through countless centuries, all have a common goal. Efforts are to utilize resources more efficiently. At first, abusive and glutenous, always more and more. But eventually, natural forces place limitations. Make corrections to unchecked human behavior. That is Nature. The effort is to promote, uplift, and establish an identity; the identity of Man. That is Man, and each man. Human desire, and hence behavior, is in opposition to nature. Nature does not care about a PERSONAL you. It is only fair: You do not care about Nature and Nature does not care about you. But man walks in resonance with Nature, on condition, with a tenacious treaty; and it is just to even exist. All rights revocable at any time. No reason.

I have made an observation in the past about hypothetical advanced civilizations. Admittedly, No one else thinks like this, at least that I am aware. But I am right. I am so right! The fate of progress, the fate of advancement, is necessarily one of assimilation into nature. You might ask, what the hell does that mean? A big strong civilization can be dissolved away? No! I am not saying advanced civilizations die out with a whimper. That is not going to happen, they will see to it. They do not die out at all, but rather have a huge unimaginable life, just with a different kind of "presents". What I am saying is that you can not see them with our primitive preconceived expectations.

In the olden days, man gathered resources in huge physical piles and in a myriad of forms to signify his existence and presents. Man marked his presents the same as a cat peeing on everything. And just as elegantly too. With pyramids and skyscrapers man became physically visible on the land. You could point your finger at his presents. Man exploited fire, made it bigger and brighter to glorify his presents. With electricity man lighted the night. At night, man's cities are seen from space. They cover the intire globe in glorious spectacles of light. Man's nature is to garner and control natures resources, exploiting and magnifying along the way, and building with no end in sight. First the stream and then the river, then the sky and ocean, then the whole Earth, and then the solar system and beyond. There seemingly is no end to the bold presents. Power and control, done with an insatiable hunger and competent skill. At this stage, you can point your finger and say, that is man, that is human, those are people. Look! Bless them and watch them go. But it is not ment to be. Man's brilliance is only an expression of evolution. And evolution denighs the exeption.

Nature, in man's hands is elastic. Efforts only stretch Nature, with give and take. Although Nature yields and provides, it still resists the human urge. It takes effort. There is resistance. A whisper at first, a soft; "No, you can not do that". But later Nature grows a face. And declares rules and statutes. They are written in universities, in the halls and in books. Nature shares its bounty, but to a mortal in a cage. And that is the sad truth: Any infraction is met with a rule, chiseled in stone, and proclaimed with equations. Nature is holistic, remembers everything, and does not care about you. At this scale of civilisation, you sneak nothing. However, Nature does carnate Gayia and other forms of evolution, but that is another story. Nature demands limitations, and they constantly show themselves as persistent reminders, demanding mans reverence. A reverence demonstrated by measurements and calculations. Respect for Nature, in the form of knowledge, measurement, and primitive calculation has gotten man to this stage. At this stage, and with some justified arrogant pride, Man can say that he has conquered Nature. Man has confidently proclaimed this step while standing on the moon of the Earth. A large step of conquering for Mankind.

The next stage begins a thousand years past the Industrial Revolution. The computers can not grow big enough to muster enough Reverence. There is a problem: Nature has a direction of time assigned to it. There are only two disciplines that contain a direction-of-time: Entropy and Fractals. Calculable type computers can not handle this. A thousand years on, and there is still no such thing as Fractal Math. The closest thing to it, are computer languages. A cursive descriptor at best, and a wild simulation at best. A thousand years on, and Nature is no longer tameable.

from the Bible

3) What do people gain from all their labors at which they toil under the sun? 4) Generations come and generations go, but the earth remains forever. ...All is vanity. Quote from Ecclesiastes

Physics and Mathematics create Science. And Science is the tool that Man uses to manipulate Nature. But can his manipulations be recognized?

At work, in the lobby of KHSL-TV, I had made a stereoscopic viewer. And in it, I had placed a couple of my 35 mm slides that were almost identical. Almost! This was a mere entertainment device producing a three dimension experience. Waiting guests could look through my viewer. So, I took it one step further. I created a field of random dots. This could be represented by Nature. I assigned this image of random dots to be a "left image". I created another field of random dots and assigned to a "right image". I then had a computer take a subset of random dots from the left image, and place them in the right image. The subset happened to be a circle. To Nature, both images are random dots. But to a human, looking through my viewer, a circle can be seen. The circle has significance, has personal relevance. But only to the Observer! Only to the Observer! Man himself alone, by gluttonous pride, can see his existence. But to Nature, and no matter how complicated, all of man's creations are "Natural", and "expected". And are seen by a stalwart, indifferent face, of the rest of the Natural universe, as part of Nature. Man was already on the agenda billions of years ago. Nothing unusual.

A 50 cal machine gun, with brass shells and primer, and a large 0.51 inch projectile, is natural.
A 100 MegaWatt Nuclear power plant with a molten salt core using thorium, is natural.
We can not be too arrogant here...



When I was in the 8th grade I conceived of an Entropy on a global scale, a Natural Entropy. I had not even heard of Thermal Entropy, the established entropy. Briefly, mine was a changing of energy into gravity with a decreasing time-rate. Time-rate was its measure. What makes me and my theory sound stupid is that the transformation degradation is not measurable. But I am still right. Anyway, I would later learn in High School, with access to better library books, that the world only knew of Thermal Entropy, and any other type of Entropy clearly demonstrates ignorance. I called my Entropy "Time", and not to be confused with, but related to, time-rate. And I knew nothing of differentials back then, but the concept was there, the same as acceleration from speed, and speed from distance, and such. I did not have the tools to do it. I wrote a paper on it in High School. By the unpleasant reaction of several teachers, I am sure it was thrown away and lost. I received very clear verbal statements of disapproval. Even if a student has it wrong, the student should be encouraged, in some kind way. An educational courtesy afforded to many; And given to students without my strong and absolute conviction. Instead, I was chastised, and the hope that they had had for me was clearly stated as gone. I was told that they had lost confidence in me. I had presented the paper to my Trig teacher, for whom I had a good deal of respect, and he shared it with the rest of the staff: my physics teacher, my biology teacher, and the algebra and math teacher. Only Mrs Sliger, the math teacher, still had confidence in me, and happily, it was strong. Or perhaps, that was because she had Carolyn, my sister, in her class. Maybe, it is zero out of four.

Anyway, I feel that Fractals play a part in my Grand Entropy in an unknown way.

Here is my point: As the centuries go by, computers grow bigger and bigger. And still they can not do the calculations. With breathtaking exponential growth, they hit a brick wall. In fact, in a practical sense, they can only become WHAT they are measuring. Simulations become impossible. It has to be the real thing. And further, as computation and information become more of the physical reality, then it follows that any lifeform must be more highly tuned to its environment for reference. Divergence is easy. Fantasy is easy. But the lasers and cooling fans are not. The damn Simulator is 10,000 times bigger than the Dam. Nature becomes the road block, the one and only constraint. An advanced civilization must deal with the Nature problem, to advance any further.

Nature itself lives on, but it produces Life and death, products are born and reborn; Nature's hand is always changing, growing and morphizing. From a human perspective everything rots and sours and constantly changes. Perhaps it is easier to change ourselves than to change Nature. Can not get around it. But you realize that it is the results of Nature that are changing, not Nature itself. A fractal does not change its nature. Almost by definition, a fractal does not change. But they produce ever changing beautiful patterns. Even Groups of Fractals, that produce unfathomable complex natures, do not change. You are not going to change subatomic particles, nor atoms, nor the nature of planets. Such beautiful results!

But, what if, you can change your body to agree with Nature? If you can ride the horse, Nature is immortal. At least immortal for 10 to the 14 years. Physical immortality may not be the holy grail, but it is a second best.

An advanced people at this stage, must give up something to achieve immortality. What do you give up? Your blood? Your bones? Diehards relinquish a few pieces; The absolute minimum to still keep love and sex, desire and passion, and muscle and beauty. The old ways of ancient heritage... The ways of the ancestors... The natural ways of organic DNA...
But the handwriting is on the wall; Robotics and Automation are all over the place. They stand alongside humanoids that have made a complete transition. And they have new artificial desires, created and discovered, along the way, in the world of Games and in the minds of fanciful Code writers. And it is passion just as strong as biological passion. And with the same effects of a drug. The Earthly passions of our ancient youth are now relegated to a mere option. Such artificial passion is only, and can only, be sustained in the long term by the support of Nature. A passion is thrilling because the course is fully known, with the experience new. The experience is different and becomes exciting. In other words, it is a fractal, without calculation, and indeed, can not be calculated. Parts known and parts not known. It can not be calculated, and becomes the perfect ophioid. A fractal in Nature is Real, and the ultimate in familiar unpredictability. The nature of a fractal carries on for ever. It kind of lives; with a machine life of its own. In those days, code-writers become zoo keepers of caged fractals.

A cerebral passion is separate from Nature, and will die from Entropy due to the necessary physical support systems. That is the worst part, but also uses calculating computers; and their course is limited and known. Therefor, death also by cerebral boredom in the long run. But if a long life is not expected, a short virtual life can be extremely exciting. Today, a vicarious experience, with some kind of sensory TV, has a lot of value to your present existence, but you are still going to die. Being with Nature is key. If you are not highly tuned into Nature, you die. That has always been the case. And in this particular case; you are PART of Nature. Not only do you have an immortal ride, but also immortal identity and a strange control that I am not able to describe. I have experienced it, however. For example, when my father died, and also when my brother died, and when Linda's son died, and when a friend died. They, or an angelic agent, representative, angelic delegate, or an angel, do indeed, have some kind of control. But that is a whole different story, and not this topic...


What is invironment, and what is the lifeform?

My crazy claim is that any advanced lifeform becomes nature itself. But it is not bad: You still have identity. You have will and power. ...And of course, you live in bliss. It does not matter what Nature is, the lifeform will become innately part of it, if it is to be successful in an existence.

Here on Earth, a short term indorsement by Nature is possible. A short term indorsement is what we have today, with a slow death at the end, from entropy. It is cheap, and is easily achieved in Nature. It is a throw away lifeform. Almost, an after thought. But a thousand years on, and you can throw a lot of money at it, and the principle will not change one bit.

Through science the human body must change in ways more agreeable to Nature. More to the natural fractal type of behavior of Nature. As an additional tool, calculatory Math, with equations, will give way to Fractal Math. More with propensities and innate properties. "Wave Equations" as "Classes" yielding existence and instantiation. Just as in quantum science, your body will not be known entirely. Your body will be subject to change, just like in Nature. Your body will never be rigidly defined. Once a body is rigidly defined, it has a finite lifetime. That is the price! Perseverance and self preservation have a new and eroded meaning, as identity becomes one with Nature.


On the other hand, today, a body can never totally escape what one is born from. Born from it, operate with it, and finally succumb to it. Nature! Once a body is rigidly cast in stone, for example, it is subject to the insults of Entropy. There will be thirteen gaskets to replace, and a replacement of more fresh blood and bone. You could give up, and say; That is just Nature. It wins in the end. Or you could say there is more to Nature than Entropy and a bad attitude.

A thousand years on, and there are modest gains in longevity. Your body is getting ravaged by adaptability. Pieces of metal, and pieces flesh thrown around here and there. Life has become pieces and components. And now, despite great concern, you are told that none knows for sure what pieces are you, or what pieces will be you. Nature has been playing this game for millions of years: In your left ear, you may have the same water molecules of Cleopatra. Identity becomes diluted, as a single energy in a bath of molecules. That is the price that a single molecule pays in a rich life of many. A thousand years on, and your brain and body have the same pieces as everyone else. Any transcendence is reduced to mere DNA, echoing down through the generations. Thursday you are this, and Friday you could be that, and you have lost track of which day you are you. Now hold on to your head. You have to worry about your Consciousness.

Which leads me to my next point: Consciousness and Emergence. Emergence is a natural consequence of Factorial growth in general, and Emergence of consciousness is a natural part of Nature. Atoms "emerge" from the combination of protons and electrons, "water and ice" emerges from a bland ordinary molecule, glowing "suns" from hydrogen, planets of vivid green "emerge" from supernova, and life "emerges" out of the dirt. It is not a new phaenomenon. In fact, there is a reason for it: With every iteration of a fractal something new is created. A fractal emerges and repeats with a reoccurring flavor, but with each iteration, it is a little bit new, a little bit different. Here, on this scale, Emergence represents the lower spectrum of a continuum. But with more cells, a quadrillion cells, that continuum includes consciousness at the other end. Emergence is continually on a continuum.

We have an additional problem at the high end of the scale: the creation of arrogance. A huge problem! Arrogance is a huge problem to understanding. Man has a large ego, and feels he is above his raisings. Above mud and dirt. Emotionally, he feels above and apart from Nature. Man has a stubborn and unchanging mantra. And as he stares up in darkness at the lid of his coffin, he whispers with a still breath, "I am in control.", "I am in control." ...That is arrogance.


I have written before of what consciousness is, and I should not go into it again here. Suffice to say, that it has a lot to do with static, and I define it as static, feedback in the brain; which is similar to dynamic feedback in the fractal nature of Nature. Anyway, and as I have shown with fractals in general, Emergence will feed back on itself, and modify itself, in Nature. That is what a fractal is. A fractal has a life of its own. It is like it has a spirit. As a consequence, Nature will change, change for sure, but ultimately always be Nature. And always true to itself! In fact, if you exclude extremely primitive lifeforms, like us, then if you scan the skys with eyes, or even machine eyes, you can not identify any portion of the universe as unnatural. You can even scan the Earth, and there is nothing unusual. Just natural stuff. It is like a law: Everything will look natural. And if it does not, we increase our understanding, and eventually it does. If you exclude banging on drums, rockets, and TV signals, then you can not see in the heavens advanced life forms, and you can not hear advanced life forms. But they are there. Despite any in depth analyses, ultimately you will only be staring at what is called "Nature".


The practical question arrises: How high can a sailing fish jump out of the water? The fish seems bound to the sea. How many scales does the fish have to give up to get higher? This is analogous to a missile leaving the surface of a planet with the hope of never returning. It is called "escape velocity". But Nature is no ordinary planet, it is more like a Black Hole. You have to give up EVERYTHING and become light to escape. ...if at all. There is no Escape Velocity from Nature. Sort of like becoming Nature itself. This is the dilemma of an advanced civilization. The height of the jump is inversely proportional to the uniqueness of will. The more you want it, the less high you can jump. Nature allows a maximum height, and if your will is in agreement with natures will, you can obtain maximum height. So if you still insist on your personal will, you are going to give up a lot of fish scales, and may not even look like a fish. If you can not fight it, perhaps it would be better to join it.

As a personal note on being human:
It is rare for me to take this emotional position, so I am going to have to overdramatize to make my point. But it does happen, and needs to be expressed. It is a human thing...

I have always wondered why Nature is so uncaring. Why is Nature indifferent. Nature does not seem to care if you live or die. In fact, Nature does not care if anyone lives or dies. Turn on the news. Nature has a disturbing feature: all day long it caries on a profoundly solemn business. I am a very caring person, I don't understand. Like reaching down and picking up a dumb rock. What are you going to do with it? Throw it? And later in school, mathematical equations, in themselves, express that same solemn matter-of-factness. I have been perplexed, like when you look to the heavens and stars, that there are no bands playing. Nature at night just sits there, as a deaf mute. Even when Nature is doing something, it is only a wheel turning another wheel, and that one turning another. Pointless and boring. Inanimate things doing a melancholy business. As a conscious person, you can reach out your capable hand, and you can take Nature; use it, shake it, stretch it, do anything to it. It is up to you. You can do anything, it does not care. Nature plays dead. For eons Man has seen Nature as an inanimate thing. Only there to be used. I can make an arrow head out of a stone, and put it on the end of an arrow. Look at the "arrow head"! It does not care. Or, is Nature mindless to our stupid little definitions. If you are an engineer, you can change the course of a river. It does not matter. You can do whatever you want, to this dumb stuff. From appearances, I am the potter, and Nature is the clay. Ever sense I was a little child, I have looked for the consciousness in Nature. How can I emerge out of this dumb stuff? After all, I have never seen yellow mud turn into something it is not, like gold. Not ever! Emergence can not be that damn simple! And especially emergence of me. And if Nature is conscious, like me, what kind of a sick game is this? ...Because it be kinda lonely here. As long as we grow old and have blood in our veins, we occasionally see a lonely, dark side, that we can not shake from our gut. We are a mire lonely shadow, divorced off from absent parents.

I have been overly dramatic. I actually only see this dark side very rarely. Normally, when I look to the heavens I see breathtaking beauty beyond bounds. And mathematical equations come to life with shouting and glorious proclamations. The band plays beautiful songs. Equations are emotionally uplifting. As a general rule, for me personally, mundaneness is disgusting, a psychological illusion. An illusion, both emotionally felt, and also known logically in the noggin.

As I have shown with fractals, fractals are not dead. Fractals in my article, as you can see, produce very beautiful detailed pictures. And Fractals in Nature produce very beautiful detailed pictures too; as things. Look at flowers! Nature is not an inanimate object, that you can kick with your foot. That rock is just as alive as your foot! It has a spirit. If that rock could be transformed to canvas, it would sing and produce the most beautiful pictures.

For example, blink once every thousand years. And look... You can not see it with the eyes that you were born with. Those are biological eyes. Evolution gave you no need to see this, with those eyes. Evolution wasts nothing: no need, no have. Your need is to survive and reproduce; not in looking at rocks. But the spirits are there. You just can't see them. An advanced civilization can see it clearly, and more importantly; can feel it. Nature has a solid unchanging sole, with a consistent agenda, but produces the most exquisite variety in a myriad of ways, always changing, and always never satisfied with the present beauty. There is another beauty, and another, and another... It will be a hard horse to ride. Fractals in Nature, and Nature itself, have escaped the bonds of Entropy. Entropy can not touch Complexity; two independent variables. Complexity is not Entropy. Nature is alive. Nature, and all that it contains, has an underlying spirit. Pervasive, bright and expressive, to the ends of creation. And, more importantly, it is bigger than you. You are not the center of the universe. Get over it.



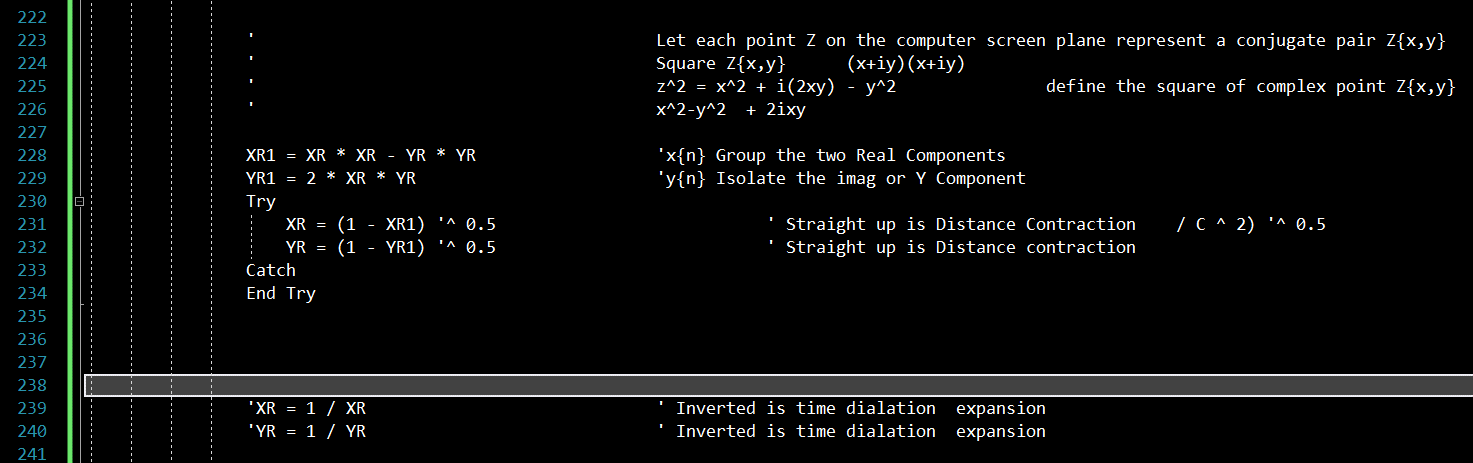
Here is the "Distance Contraction" code.
Velocity is assigned a complex number. xr for real component, and yr as imaginary
Not shown is the criteria. The criteria is XR, the real component, to be less than .5 the speed of light.
.5 Squared is .25. C-.25 is 3/4 speed of light. Looks right...
The black areas are when the criteria is met immediatly, with no iterations.
The brighter the color, the more iterations to make the criteria happen.


Looks like intestines in car metal.




Here is the same display but with square root of the term (1-v^2/c)^.5 C is one and not shown.
Taking the sq root really squishes things down.


Looks like tree branches.


Anyway...
All of the Fractals displayed above are only pretty pictures. And they are full of artifacts of my arbitrary criteria.
And why would one create a fractal by putting a derived Lorentz back into itself?
So, to return to the original problem of calculating the Lorentz at, or near, the speed of light.
The Taylor expansion is not useful at low velocities, and can not be used at the speed of light.
So, this is a problem...







I have to interject with a personal story because Entropy is so important. In our world, entropy causes time to progress. Well... Only with my Grand Entropy, not thermal Entropy. Anyway...
There is another world where time does not exist, and strangely time is used for communication between the two worlds. At least I am going to assert the notion. It is vague. Iffy, and raises eyebrows. The strange notion involves a story, and time was used in this story...

My brother was killed several years ago while ridding his motorcycle. He lingered two weeks in intensive care before being taken off life support.

Before his death, my brother and I would sit on my couch, always staring straight ahead at a painting, and dreaming of riding motorcycles in Maui. The picture was actually a beautiful oil painting, painted in Maui, and we called it "Paradise". We both loved to ride, and planned to ride together in Paradise, in the ocean breeze among the swaying palms and green ferns. During his visits to my home, the picture was a natural focal point, the epidemy of what we loved. We loved nature, beauty, and especially motorcycles and riding.

Picture taken in a different year: 2016.07.24 The painting near the time of injury. July.24

Ben was killed while riding on July 20th 2014. After the news, Linda and I were sitting in the living room, terribly somber and sad. I on the couch in front of the painting, and Linda to the side. Suddenly the painting lit up. We both stood up and looked in disbelief! I went closer to it, stood in front, and dispelled the notion of capturing a picture with a camera, as this was, in my mind, sacred and special. But no, after hesitation, I decided to get a picture of the event anyway; for my brothers and sisters. They needed to see this too. I was able to get two pictures before it faded away. Also, I was able to determine the light was coming from somewhere in the kitchen. The next morning, the painting briefly lit up again at about the same time. And now, I knew the light was coming from a high kitchen window. This was the first year that light could come through, at this time of day, because several months previous, I had cut down a small and narrow oak tree, that had been blocking the window, in a very special way. So, this was the first year and time this could physically happen, if it was going to happen. But, of course, it does not matter "how", only the "why" matters. However the precise nature is astounding: only the picture was lit, and lit exactly only during the time Ben was in the hospital. During the two weeks, the light would progress from right to left a little each day. First lighting the shore, then the waves further out to sea.

A different year... The painting at the end of the two weeks. 2016.08.05

Ben was brain-dead, and after a somber and formal meeting with all the doctors, we sadly agreed to take Ben off life support. Ben officially died August 4th. The picture stopped lighting on the 4th, and had just a little light on the 5th. I was so grateful to Ben for letting me know. The grief would have been unbearable without our personal Paradise painting. He, or an angelic agent, choose a sign wisely, that I could understand. I had been communicated to, by someone in such an undeniable fashion. And time, in the form of dates, was used.

Ben's injury was on July 20. The picture generally began lighting on the 20th or the 21st of every year. The picture continues lighting to the 4th, 5th, or 6th of Aug. The picture lights 15 days, most every year. Due to the Earths movement and inclination, the picture would light this way forever, in theory. ...As long as the picture is still exactly on the wall in the same place, and the house is in the same geographical location.

In the year 2020 my theory was changed a little:

I had a tooth extraction. My tooth was extracted on July 28, followed by sevier pain until Monday Aug 03. That is about a week of pain in the larger time frame of Ben's pain. Ben's pain was two weeks long, mine was one week long, ending one day before Ben was taken off life support. I had surmised, that the effects or influence of a "passing" person would diminish with time. After all, when Ben died I could feel his presents and talk to him. But now, years later, I do not hear from him. My assumption seems to be wrong. Ben is back, regardless of time!

It is unconsequential to this topic of what he said. But he seems to say that it really hurt. I am glad to share his pain. I am so glad! Any day at all I will share his pain! I am his brother.

In a world of no Time or Entropy, Static Time is still used to communicate. It is a marker between the worlds. To talk requires "running" time. Everything that we experience as humans requires running time. Consciousness is a transparent flow. Consciousness, as I have defined it, requires a stream of static events. This is artificially interpreted, in consciousness, as seamless running time.


On 2020-08-07 10:46, Carolyn Winant wrote:
> Alan, you torture yourself every year at
> this time. The picture lighting up with
> a shaft of sunlight will always remind
> you of Ben. It is the same for me in
> February when the yellow Acacia trees
> are in blossom. They are indelibly linked
> to Mom’s funeral in my mind. They will
> always remind me of Mom. A comforting,
> yearly happening, a sign of life, and a
> sweet reminder and a sweet “hello”.
> A Redtail Hawk will always remind me of
> Ben. When I see one soaring and gliding,
> sometimes it seems to circle me and take
> notice of me. And I’m immediately thinking
> of Ben and smiling. We find ways to hold on.
> Carolyn
>

Carolyn;
What you say is true, but no, this is not my focus.
I am an Engineer. For example, I spent about 15 minutes this morning exploring HOW the picture is no longer lighting. I already know WHY: it is from Ben. So, at lest in my mind, from a technical standpoint, this is not a natural event. For years, I was thinking it may be the "Butterfly Effect". It is a measurable and notable outcome from an incredibly small force. But no. No matter how exact I measure the light paths, and angles, from the window, to the stove, and to the picture, there is no manner that opens itself up to the Butterfly Effect. No, it is not a matter of magnitude. And in fact, I can postulate that the "mechanism" can NOT be found. Therefore, the communication is one of Consciousness and Entanglement, possibly from Ben and I sitting and looking at the painting. An established physical pattern of using the painting as a focal point when dreaming of a "motorcycle-ridding Paradise". Remember, I have always said, that one can not see with the eyes, until first one sees with the heart. Site deprevation of babies at birth prove this. First they must have an emotional "sight" from the heart. Otherwise, they will never see, even with perfect technical vision. It is merely a technical requirement for the eyes to move back and forth, and to focus and such.

Ben has left a physical event that will now reoccur every year as a personal reminder. But it can only be seen by your eyes and my eyes. A stranger can not see this at all. Forget about the legacy; they can not see it even one time. For others, it is undeniable and absolutely breathtaking event when you see it with your heart!

Alan














Email to C.A.Pennock