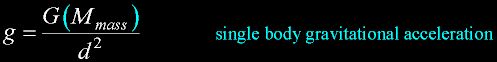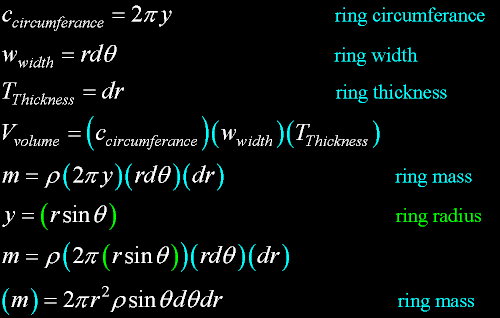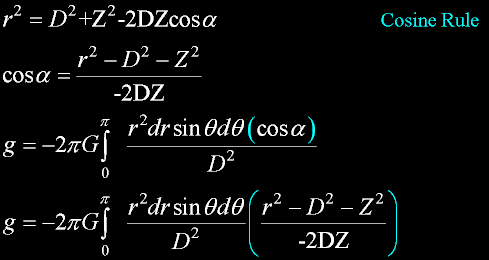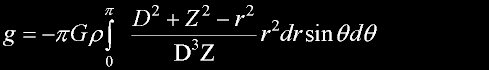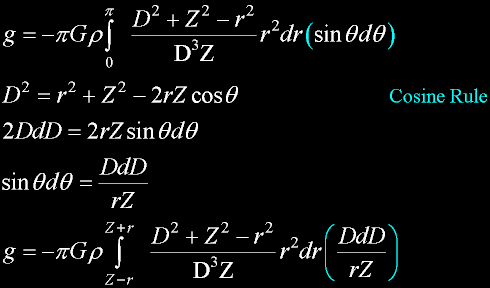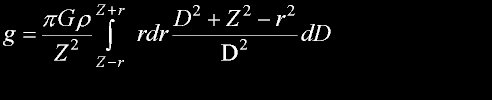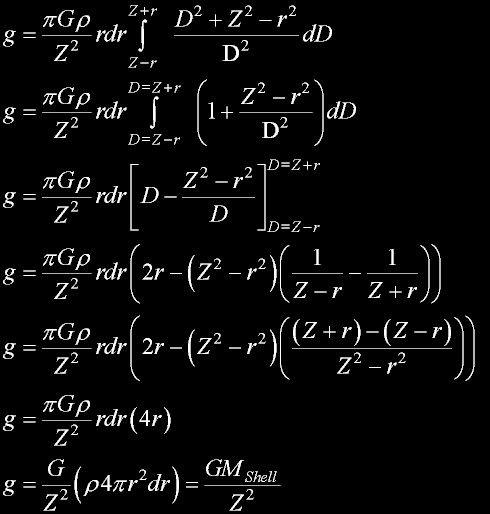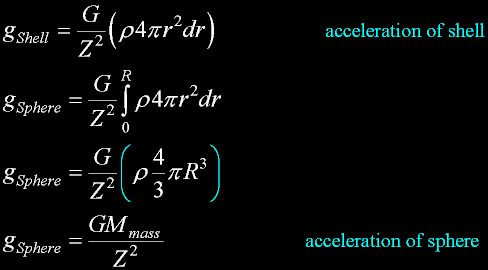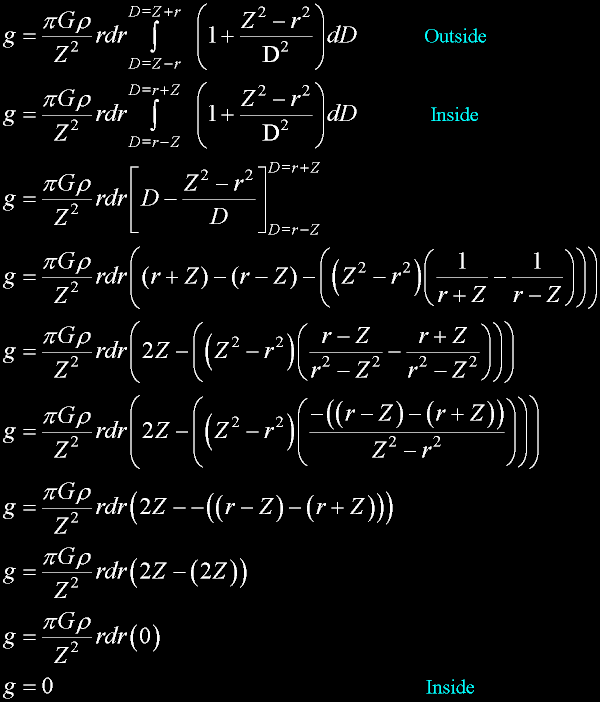|
|
Field Geometry of Spheres |
|
Electrostatics and Gravity, and Shells and Spheres
The anatomy of the sphere must include density. Density, wether of mass or charge, is innately
involved with the "physical" geometry.
Also radius is no longer a constant. Its treatment needs to be a variable for the integrations to
proceed.
First, We would like to consider a hollow sphere - or shell...
Of constant density.
Here is the mass of this shell covering the intire sphere.
One intuitive,
The other derived.
We choose to leave shell mass in the deferential form because of a convenient integration to
obtain total sphere mass made up of successive shells.
Treat this as an identity for now. (I will not integrate it while working in shells.)
The ring shell, as well as the intire shell, has this thickness
(This is a trivial thing. I don't think I will use it.)
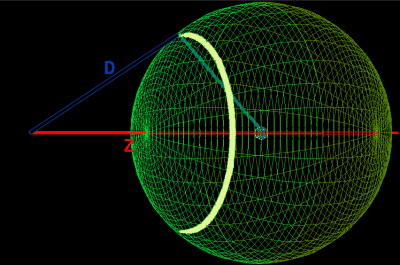
Diagram
|
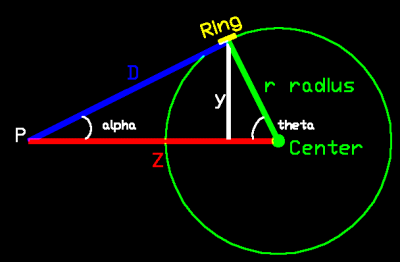
We will use this diagram:
An observer at point P.
The observer will be measuring acceleration or force
from composit masses in the form of a sphere.
A distance Z from the center of the sphere to the observer at point P.
The center point of the sphere was chosen on a "hunch".
It is a secret for now; later to be revealed and later to be convenient.
Z is a constant.
A distance D to either infinitesimal masses or charges.
The distance D is the operating line for the actual field laws.
Distance D is a variable.
The radius r of the sphere.
At first, r may not seem a variable. But my treatment throughout is one of a variable.
Radius r is a variable.
Acceleration g equation:
Follows the inverse square law. Purely a geometrical law, where distribution
is the only cause of attenuation. But there I go on a different subject...
The mass in this equation can be considered a single body "point-mass"
(of which there is no such thing, but that is another story again.)
The lower case d will become the upper case D when we start to integrate.
This is the accepted generic gravitational equation that we will use as a starting point.
Before we begin, I would like to emphasize one more thing...
Shown is my crude but dramatic aid in vector visualization...
The observer has two large masses abreast. And one mass straight ahead to observe.
The two masses to either side are extremely dense and huge in diameter.
Yet they do not influence the observers measurement of force or acceleration in any way.
It is like they do not exist!
Force and Acceleration are vectors. And as such, in this example, have their lateral
components cancelled.
Superposition explains this with beautiful mathematics; But
- psychologically - not to feel the presents of a couple of monstrous bodies can be quite unnerving.
Therefore - and to not use vector algebra - we can, thanks to symmetry, use only
cosine acceleration - which is the straight ahead component.
The deliberate construction of rings has allowed this symmetry.
Rings
Each incremental circular ring shell has a volume and a mass.
Substituting incremental mass into the acceleration g equation...
We have too many variables...
We should gravitate toward Z.
(Sorry for the inappropriate pun.)
...And retaining ANYTHING of Z. It has something to do with
that secret I mentioned.
Use the cosine rule to eliminate cos(alpha).
Good trade: we gained a Z, and eliminated cos(alpha).
Don't worry about dr. I am only going to use it later in an identity; and not in any integration.
We can eliminate more...
The derivative of the cosine rule will allow a sin substitution, and
eliminating the sin(theta) variable.
A third objective is a better integration variable...
Change integration variable from theta (zero to pi)
to
D: (Z+radius to Z-radius)
Here is why I kept the derivative form.
It is so easy to integrate the shells into a solid.
Just stack the shells like an onion.
I forgot to mention the secret (if you havent noticed), and why Z was so carefully maintained:
In electrostatics and gravity, and with shells and solid spheres -
all mass can be represented by a POINT: the center of mass!!
Something interesting happens when we make Z less than r.
In other words, take the observer inside the sphere.
We have to change the limits, but that is all that is necessary to look
inside the sphere shell.
Weightless!
Just because of geometry!
Their is NOTHING else at work here. Even inverse-square force and accelaration
are due totally to geometry.
I believe that Newton himself proved this with just a ruler making a couple of lines
in a circle. Newton was obsesed with geometry.
It makes one wonder how many more physical laws are due solely to geometry...
Use the other equation (outside) for all remaining shells (if any) where the observer is outside.
Both forms are continuous and compatible.
Update:
I have just now came back to this page, a few decades later.
I am impressed with the algebra.
I am impressed that I wrote a program to draw the spheres.
But more impressed with the notion
that "Physics" is really Geometry.
I have always been intrigued with this notion.
I am older now, about 73, and I would add that Fractals also play a role in reality,
but even they can be expressed as Recursive Geometry.
Also, I see the two large white masses, that I also drew.
They are almost out of place!
But I know why they are there, and what I was struggling with then.
I know what I was thinking...
Back then, I knew that gravity acceleration, and force etc, were vectors.
And as a consequence, could yeld zero gravity inside a sphere.
Just like there is no charge inside a conducting shell.
You could just float around inside a hollowed out center of the Earth.
That is true, as my equations show.
But now I know why my feelings of other aspects of gravity...
For example, Time Dilation. And, in my opinion, that gravity's Time Dilation is a scaler.
Back then,
I had a feeling that the presents of such mass could not be ignored because of mere mass configuration.
Clearly this was in my mind. I know; I am the one who wrote it, and created those two stupid masses.
Now I am older. So here it is:
As you float around down there, you can look at your watch and it will seem just fine.
But when you get back to the surface, it will be slow.
Professional physicists disagree and do not believe this.
They would argue that when you get back to the surface,
your watch would be fast, just as if you had been weightless in space, far away from Earth.
Makes no difference if you are weightless in space or weightless in the center of the Earth.
But it does! I just can not prove it. I would argue that the profeshional physisists,
weightless in the center of the Earth, can not see the mass that is all around them. They are blind to it.
If you turn out the lights, they can not see all the mass.
They blissfully float around in mass that is hidden to them. They are ignorant!
