|
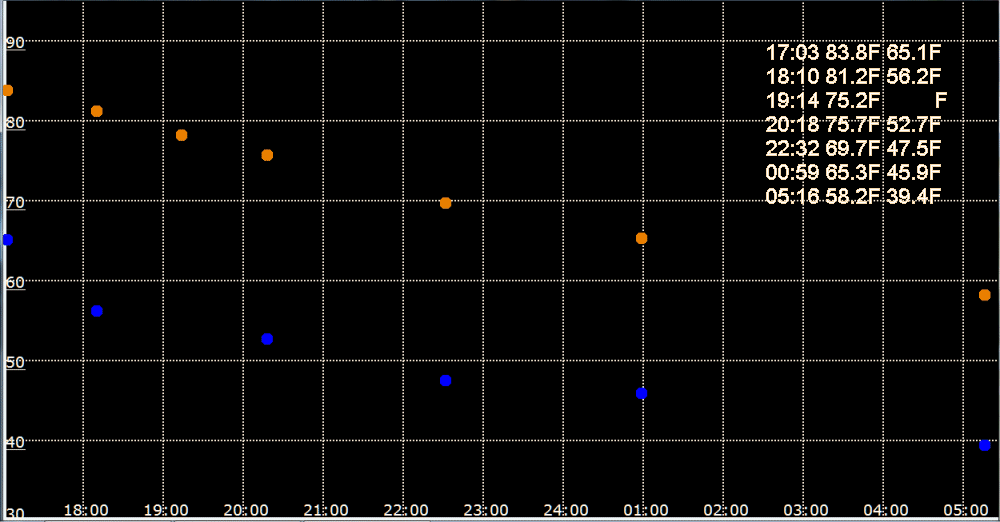
RV Maintenance Thermal Efficiency 3 |

|
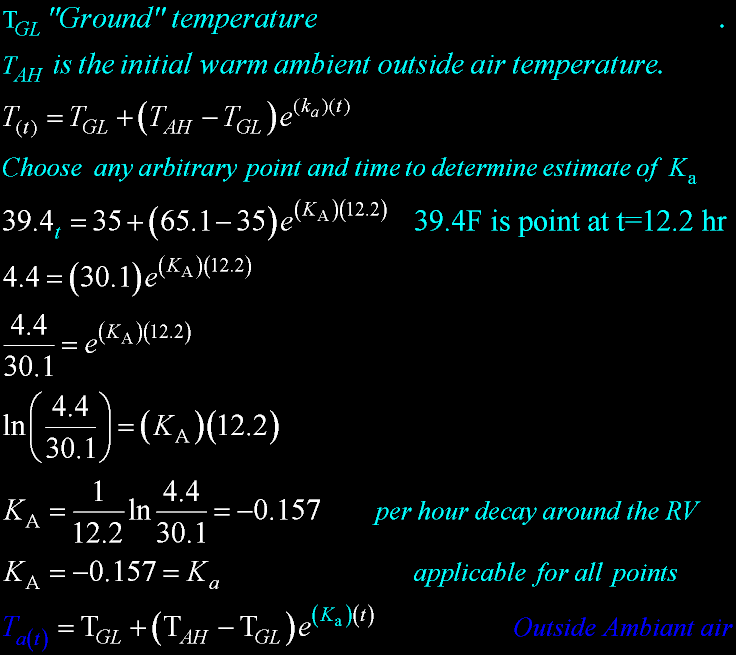
|
|
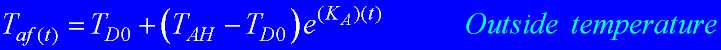
|
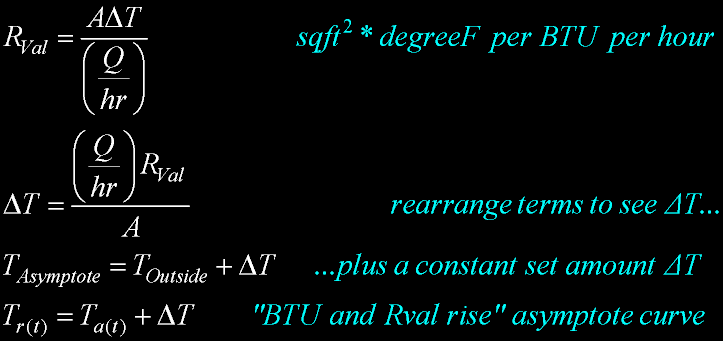
|
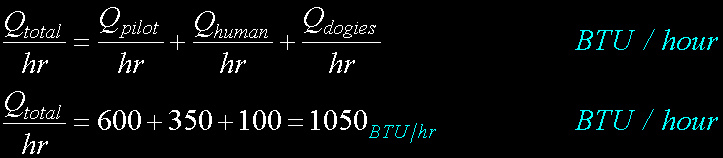
|
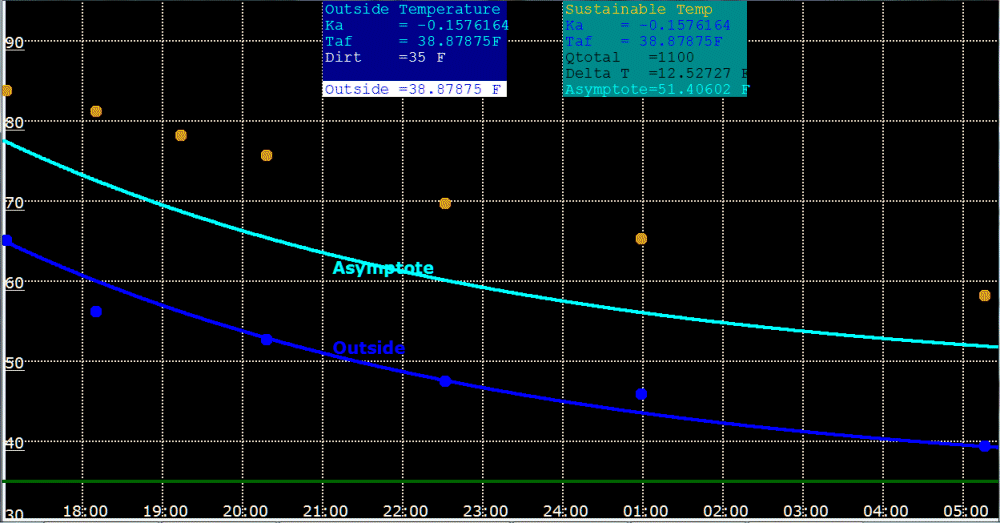
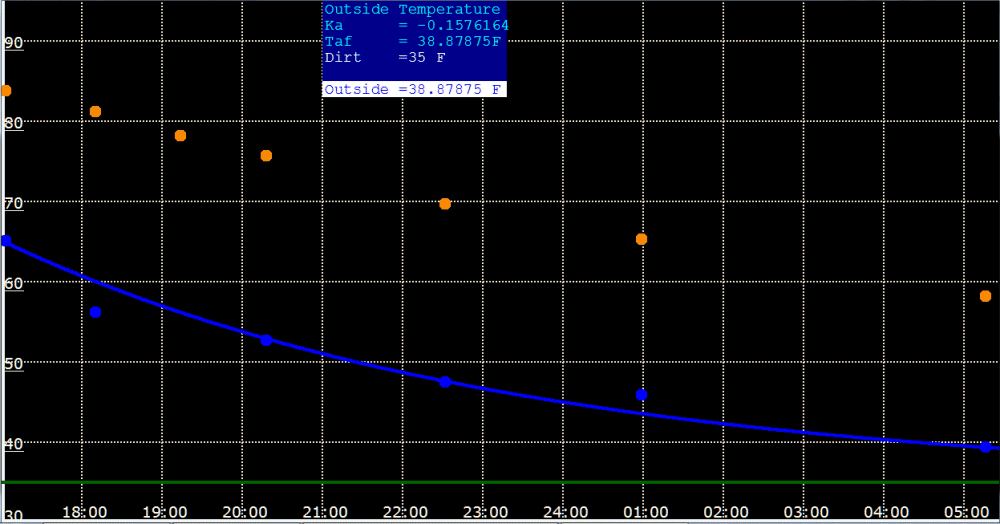
Asymptote curve. |
|
|

|
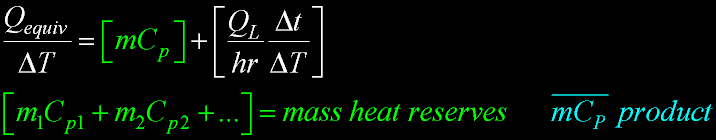
|

|

|
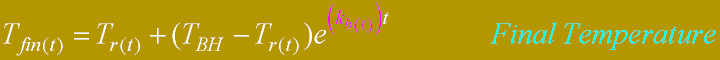
|
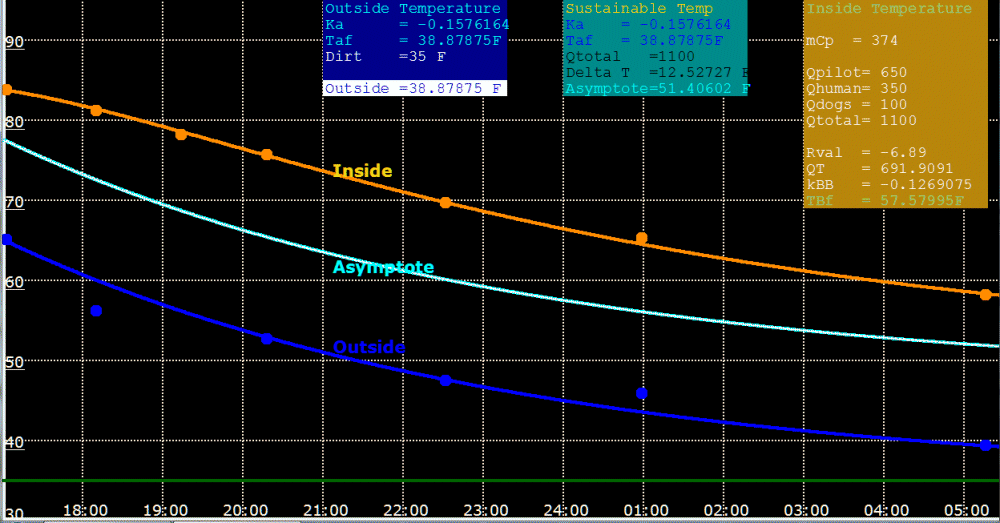
|

|
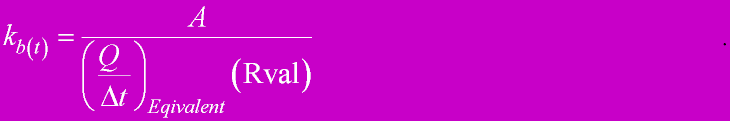
|
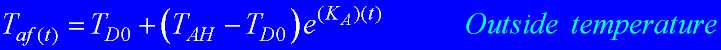
|
|
|

|

|
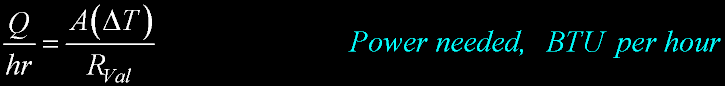
|
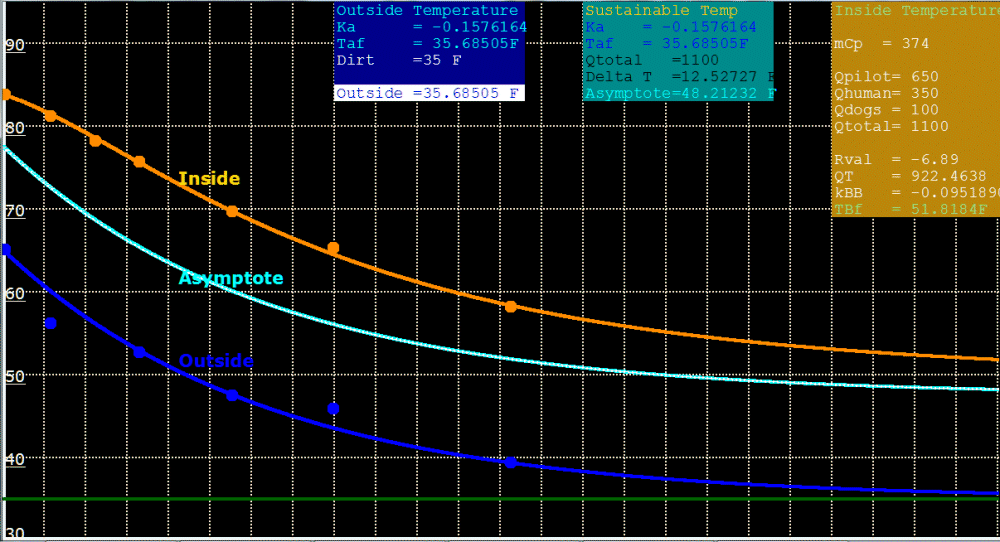 Extended graph
Extended graph
|
 Now clearly, with the graphing, my trailer is fixed and it is working great as it should, at least on paper.
Can't stand to have a broken trailer due to a faulty cooling curve.
With the equations done, I have the perfect excuse to test out the equations and the RV
at the ocean or a lake.
It is just the right amount of excuse. Not too much.
Time to go. Gotta get gas and get it hitched up first though, then decide where...
Now clearly, with the graphing, my trailer is fixed and it is working great as it should, at least on paper.
Can't stand to have a broken trailer due to a faulty cooling curve.
With the equations done, I have the perfect excuse to test out the equations and the RV
at the ocean or a lake.
It is just the right amount of excuse. Not too much.
Time to go. Gotta get gas and get it hitched up first though, then decide where...