index


( Primes):
Primes):
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47,
53, 59, 61, 67, 71, 73, 79, 83, 89, 97
101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 173, 179, 181, 191, 193, 197, 199
211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293
307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397
401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499
503, 509, 521, 523, 541, 547, 557, 563, 569 571 577 587 593 599
601 607 613 617 619 631 641 643 647 653 659 661 673 677 683 691
701 709 719 727 733 739 743 751 757 761 769 773 787 797
809 811 821 823 827 829 839 853 857 859 863, 877, 881, 883, 887
907, 911, 919, 929, 937, 941, 947, 953, 967, 971, 977, 983, 991, 997
1009, 1013, 1019, 1021, 1031, 1033, 1039, 1049, 1051, 1061, 1063, 1069, 1087, 1091, 1093, 1097
1103, 1109, 1117, 1123, 1129, 1151, 1153, 1163, 1171, 1181, 1187, 1193
1201, 1213, 1217, 1223, 1229, 1231, 1237, 1249, 1259, 1277, 1279, 1283, 1289, 1291
Used Primes:
 2,
2,  3,
3, 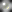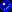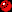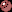 5,
5,
 7,
7, 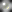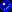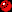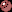 11,
11,  13,
13,
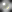 17,
17, 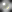 19,
19, 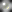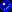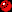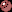 23,
23,

Ulam spiral:
The Ulam Spiral is a nifty graphics to show locations of primes. Probability of primes located
on diagonals is shown. I have written several programs that investigate not only primes but
prime factors of numbers.
 Numbers to 10
Numbers to 10
|
A Counter clockwise Ulam spiral of numbers 1 to 10. Number One is in red.
 Numbers to 101
Numbers to 101
|
Numbers 1 to 101. Number One is in red, and all primes are in bright white.
 I wrote a program to display all numbers to 20000 in an anticlockwise spiral.
The primes are in brightest white.
Numbers in brown are not prime. Numbers in white are primes. As you can see, there are patterns!
In my computer algorithm I used a quick and trivial method to derive the primes: If the number under test can be divided by any number
less than half the test number with no (or tiny remainder) then it is not prime.
Also I choose to include zero, and also to assign 1 as prime.
I wrote a program to display all numbers to 20000 in an anticlockwise spiral.
The primes are in brightest white.
Numbers in brown are not prime. Numbers in white are primes. As you can see, there are patterns!
In my computer algorithm I used a quick and trivial method to derive the primes: If the number under test can be divided by any number
less than half the test number with no (or tiny remainder) then it is not prime.
Also I choose to include zero, and also to assign 1 as prime.
I just wanted to point out that primes have a kind of sudo and tenuous relationship
that is not definable in a precise way. But primes, as you can see, are related.
The trends for favorable areas follow quadratic equations.
When viewing the straight lines, One can not help but be captivated.
Such an intriguing display, I believe, is related directly to entropy, and also in an obscure way to
inspired numbers of the bible.
Composite numbers can not be well understood until primes are understood.
 Numbers to 4000
Numbers to 4000
|
The central white dots only extended so far. They are 201 primes.
But what is interesting is the color:
The first 201 primes are assigned one of eight colors.
All numbers to 4000 are "test-divided" by the first 201 primes.
If the number is a prime, then the color is bright white.
When the division is even with no remainder, signifying a factor, then a partial color is assigned the number according
to the divisor's assigned color.
Each composite inherits some of the parents prime colors.
There is a lot of red because the prime of "two" was assigned a
reddish color. And half of these numbers are divisible by two! If a number is divisible by several
"twos", like eight or sixteen or (2^n), then the color grows in that color. The change is in brightness.


 Numbers to 10
Numbers to 10
 2,
2, 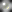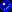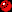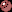 3,
3, 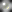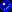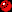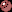 5,
5,
 7,
7,  11,
11,  13,
13,
 17,
17,  19,
19,  23,
23,
 Numbers to 10
Numbers to 10
 Numbers to 101
Numbers to 101
 Numbers to 4000
Numbers to 4000