index

How do calculate Miles-Per-Gallon when pulling a Trailer?

My wife and I, and the Woofers, have been RVing for over a decade. And only recently, while looking for a new truck, have discovered a critical error in thinking about "MPG". What if I told you that fuel economy has NOTHING to do with the MPG rating of the Pull Vehicle?

Before I get into the math; What if I told you that a modern 24 MPG 2.7 liter, dual supercharged truck will get about the same gas milage as an old 19 MPG 5.2 liter truck pulling the same trailer? For an average 6,000 lb trailer, they BOTH will get roughly 10 MPG. (My analogy must keep the energy source the same; gas or diesel.)

What Pull Vehicle do you buy? Does it make a difference?

For years I thought that the gas milage of the truck was a factor. Technically it is slightly true, but the economy of the truck pales in significants to the demands of the trailer. With a huge sail behind you, and with a huge wind resistance, you will burn a huge amount of gas - as a matter of physics. No matter how you dice it, that trailer will independently demand a lot of gas on its own.


The first step is to separate the truck from the trailer, and assign a gas consumption to each. Yes, in the case of the trailer, it is somewhat artificial and contrived. The reason, of course, it does not have an engine. But mathematically it is using energy. For the most part it is aerodynamic wind resistance. And this drag is costing gas. It is costing gas, and it does not matter where the engine is located. The price must be paid. It is just physics. Physics demands payment if the combo continues down the road at the same speed. The law is unbreakable. This law concerns only aerodynamics, friction, and even sound. Another law involves Kinetic Energy and momentum of the truck and trailer. I will get into that law later.

Fortunately, we do not need to calculate directly, for example, the energy for my 70 sq ft frontal area, in a 60 mile an hour wind, wind on the sides of the trailer, or the drag of the box on top of the trailer, which is called an Air Conditioner. The specifics are way to involved, and it would take a supercomputer to solve. The solutions are easier than you think, and probably not at all what you are thinking.




Now for the equation;

I will create it using an analogy of a freight train, and 100 boxcars, and a caboose. Each - and every - boxcar is individually consuming diesel. Every boxcar is different. And the caboose, with its own aerodynamics and wheel friction, is consuming energy too. The whole train is just a summation of individual consumers. But at this point you do not know what they are. All you know, after talking to the engineer in the engine cab, is that he is burning 2 gal of diesel fuel a minute, for the whole train. Notice, that in the equation, I place no emphasis on the engine. Nor its location. The engine, boxcars, and caboose are all treated the same. All consume diesel. In the equation, one simply adds up all the diesel fuel, or gas. The individual fuel consumptions can be in the form of gallons per mile, or knowing the speed, gallons per hour. It does not matter. The total fuel consumption will be the addition of all the consumers.

A better example would be a long train with dispersed engines. For example, two engines in front, two dispersed engines in the middle, and one at the end. Distributed power allows the boxcar couplers not to be exceeded in strength, and distributed locations prevent rail wear and stress in the curves. You do not calculate using the gas milage of any specific engine - it does not matter. You calculate by measuring the fuel consumption of each engine, and adding together, to get a final fuel consumption of the intire train. My Dad worked for Western Pacific and knew this stuff. The point is that you could also put an engine in every single boxcar, and just because one boxcar gets 1000 miles per gallon, does not mean the whole train gets 1000/gal. Only salesmen can add gas milages like that. Not even an army of mathematicians can do that.

That is not the only thing that salesmen can do; There is a bigger thing, and salesmen are powerful to use it. Once you get into the office, you will find that salesmen can change history! Not even God can not do such a thing. Wow! That is impressive.

Getting back to the truck and trailer...
But fortunately, in this situation, we are only talking two variables: the Truck, and the Trailer. This will be easy, as we have all the information.


The proper way to look at this, is to give each, the truck and the trailer, their own "gas-milage". They are each causing the consumption of gas, which is the reciprocal of MPG, which is GPM. You are already familiar with Miles-per-Gallon, so it is easy to get there. If the distance is the same, the two gas consumptions can be added, with a common denominator. This simplifies things. The equation is saying: add this amount of gas for this thing, and add this amount of gas for the other thing... Also, let us pick a specific speed. That simplifies things further, as resistance is quite nonlinear. Every speed will drastically affect the milage. To simplify things, I will aim for 60 mph.


I will put in two sets of values, which I measured, and see what happens...

The truck gets 20 MPG HWY by itself. And 9.6 towing. Therefore, working the equation for the unknown variable, the trailer is "18.5 MPG", or 0.054 Gallons Per Mile.
The van gets 19 MPG HWY. And 10 MPG towing. Therefore the trailer is "21 MPG", or 0.047 Gallons Per Mile.

The problem is that the Trailer (T) has to be exactly the same in both scenarios; pulled by the truck, or pulled by the van. It looks like my equation is wrong. 18.5 is not the same as 21!


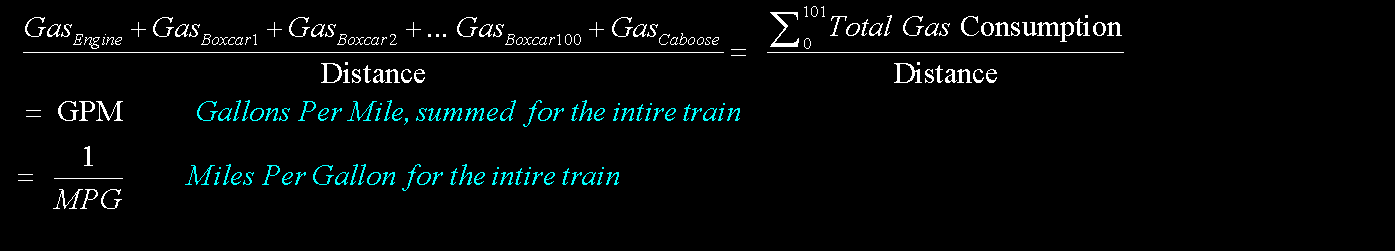
Here is the Truck and the Van - side by side.
The truck is a new Laramie 1500, extended Towing mirrors, Tonneau Cover, Short bed.
Van is 1997 extended roof custom.
The High Top van is higher than the truck. Still not as high as the trailer, but provides better pre lift for the air. Also the van provides better continuous air flow to the trailer acrose, what would be, the trucks bed area.

Clearly, the High Top Van provides better Drafting for the trailer. I was wrong when I said that it makes no difference of the "type" of truck. Evidently, when you include vans, it does! It makes a difference of the shape and size of the Pull Vehicle. This determines Drafting. And the distance apart of truck to trailer also determines drafting. For example, a long bed should get worse gas milage than a short bed.

Somehow geese flying in formation have this all figured out, and I am playing catch up. Ok, I was wrong on the shape of the truck, but I am still not going to be wrong on engine efficiency. It still makes no difference!



So far, there are two problems: First, we are using two different pull vehicles, but the same trailer. The trailer's value seems to be different in each case. How can that be? I think we have answered that question with "Drafting".

Second, the value of 18.5 mpg, and especially the 21 mpg, seems on an intuitive level, far too big for a big square box going down the road. For sure, if it were by itself and did not have anything in front of it, it would not get this good of gas milage.

What the equation DOES show, is this...
As a hypothetical Truck gets more and more efficient, naturally, the truck consumes less and less gas per mile. We have allowed the truck to be a variable. However, the trailer still consumes the same amount of gas per mile. Exactly the same amount! And what is more important, the trailer dominates the equation. That part of the equation is correct and very intuitive.

But the problem is that, in the two equations, the trailer MPG changed in the equations between the van and the truck. At first glance, that can not happen; it is the same trailer! So, what is going on?

The trailer value is obviously inflated. Intuitively, 18.5 MPG seems too good for a big square box going down the road. Perhaps, I should not use the term 18.5 MPG. It is confusing. I should use the reciprocal: 0.054 gallons per mile. Same thing. The trailers burden is 0.054 Gallons Per Mile. The terminology does not help; a big square box with a frontal area of 70 square feet, can not possibly use only 0.054 gallons per mile. For example: If the trailer was by itself, and had an engine in it, like a small motorhome, it would get about 11 MPG; Maybe 10 or 9 MPG depending on size. That is a realistic fact! I have friends. And some of them do not lie.

"Drafting" is the answer. Drafting is inflating the trailer's value. When in tandem, that is what it is. Nothing wrong with the equation! If the truck was pulling the trailer with a 300 ft rope, the equation would be perfect. Just needs a modification for Drafting. The Drafting Factor would bring the Truck's mpg down, and the Trailer's mpg up.


Actually, I am going to go ahead and modify the basic equation to include Drafting.

There are four unknown Drafting variables:


The pull vehicle will be retarded a little. The retard will be different for the truck vs the van. For a passive trailer, this force will always be a detriment to the pull vehicle. I put it in the numerator for the pull vehicle. Normally, its value will be a little greater than one.

For example... I have experienced drafting, as well as any RVer, when passed by a large simi. Before the truck gets to you, and as it just begins to pass, I am pushed ahead, and my steering goes to the right. Then as the truck gets even, and as I fall behind, I am pulled ahead. And my steering goes back to the left.

The Trailer will always be pulled ahead by the tow vehicle. One variable for the truck, and one for the van. Obviously the Drafting will be different. The van provides more Drafting, and pull ahead, than the truck. The value will be over one. And I placed it in the denominator of the trailer term because a passive trailer will be pulled ahead, and its gas consumption will be reduced.

For either vehicle, the Drafting retard value , for the pull vehicle, will be much less than the pull ahead variable for the trailer. We can not assume the retard value is the same as the pull value. For example, an inefficient and non airodynamic pull vehicle will spend more energy just moving air around, and only forming a convienent wake for the trailer. and will not be penilised, as much, with a pull ahead force.

To solve these equations, I had to assume that both the van and the truck are not held back very much by the trailer. I can assume these two variables are close to 1.0.

I also had to allow the truck to be a reference, a base, a standard. And to be assigned No Draft. Its value will be a "1"." This definitely is not the case objectively; Both tow vehicles have a lot of Drafting. All I can accurately say is the van is 1.1 times better at drafting the trailer, and better at inflating the miles-per-gallon of the trailer.


With nothing wrong with the basic equation in principle...
Therefor, if you take a different truck with the same physical size, and the same drafting characteristics, and arbitrarily increase its milage to 50 MPG, 200 MPG, 1000 MPG, or all the way to infinity, then the maximum Combined milage when pulling this trailer would be 18.5 MPG. Or, in more intuitive terms, and for the equation: 0.054 gallons of gasolene per mile at 60 mph. Or, a half pint per mile with a magical truck.

And with a magical truck that uses absolutely no gasolene, the truck is out of the equation; the trailer still uses 0.054 GPM of energy heating the air when being drafted.

To be complete...
I know from years of RVing that the trailer would get about 11 MPG if it was powered by itself, like a motorhome. Or, if the trailer were being pulled by a 200 ft rope.
Therefore, I can use the same equation to figure the total gas milage with no drafting.
A 20 MPG truck pulling an 11 MPG trailer with a rope would get 7.097 MPG Total.
And to repeat...
As measured with drafting,
A 20 MPG truck pulling the trailer gets 9.6 MPG total: The same trailer is a 18.5 MPG trailer, in this configuration.


The Drafting factor for the Truck is 18.5/11 = 1.68
The Drafting factor for the Van is 21/11 = 1.91
The relative Drafting factor, Van to Truck, is 1.1





You may be wondering why I am going through all this effort. All of this work boils down to wondering if I made the right decision in not buying the Ford 3.5 liter supercharged V6 truck that gets 24 MPG.
I am not debating if this engine is the way of the future. It is!
I am not debating if the Hybrid Transmission is better. It is!
I am only interested in pulling my trailer, and if - indeed - the gas milage of the truck makes any difference.

I now have a way to estimate gas milage for any truck pulling my trailer. As obviously, I can not go down to the dealership, and hook up my trailer. Even if you bring your own hitch; No test drives! That would be rude. And I would probably be called more names than just stupid.


Fortunately, there is another way:
Running the equation...
I must use the 18.5 mpg for the trailer, and not the 20mpg for the trailer being pulled by the van. 18.5 mpg is for a TRUCK!

The equation says 10.5 using the Ford truck. Only a difference of one mile/gal from 9.6 to 10.5.
I was right! I just could not prove it. All that arguing with Sales people! Gas milage makes little difference. I just could not formulate what I was talking about in words. That inability cost me credibility. I am sure they thought I was an idiot. They thought it was simple: "Of course gas milage will make a difference! You need to buy this one!" But NO! It does not. It is a matter of physics.

I have had several sales people, in different lots, and different dealers, literally walk off from me, rather than throw the first punch. What seems intuitive to a stubborn sales person with a small head does not make it correct.





To make the discussion complete, I will list all the sources of fuel consumption:

Friction has several parts. For example:
Air Friction or Aerodynamic drag.
Road, Tire, and wheel Friction.
Noise


Altitude or Elevation change.
It takes energy to pull a trailer up hill, involving the force of gravity and the vertical distance. Several Regenerative systems can reclaim some of this height energy as well as lateral energy. In fact, in a perfect world, if you go down the same hill that you went up, its a mute point. But another point involving hills; Engine efficiency really changes with torque, like when going up hill. I will not discuss it now.

Kinetic Energy of Motion.
In the case of the momentum of the train, it includes all engines, boxcars, and caboose.
In the case of the truck, it is both the truck and trailer.
I have neglected this topic. I will include it now, despite its onetime nature.
Once the truck and trailer are up to speed, there is no more fuel consumption from this source.
On a long trip, with little stop and go driving, this factor of momentum, once established, becomes trivial and insignificant. But I am still going to include it.


You can measure this Energy by either measuring the Mass of the truck and trailer, and multiplying by one half the speed squared. Or, you could measure the temperature of the brakes when the truck was stopped. The brakes would melt in a vacuum chamber, so this is not a good way. Obviously, it is easier to simply look at the speedometer, and use this equation.

The final equation is 1/2 m v^2. The velocity was set at 60 MPH. Mass is a factor! In selecting a truck, you are selecting a mass. Also, in selecting a trailer you are selecting a mass. If the trailer was way heavier than the truck - thank goodness it is not - then the mass and gas milage of the truck would not matter so much. The truck would fall out of the equation. But personally, I like the truck to be heavier than the trailer. Now the gas consumption - attributed to linear motion - is significantly claimed by the truck.

The argument above, with aerodynamic drag and friction, attributed a lot of the fuel consumption to the trailer. It did not matter as much, about the fuel consumption due to the truck.

If you are driving a lot downtown, pulling a trailer, then the choice of truck DOES make a difference. When pulling long and steady roads, Kinetic Energy, once established, remains the same, and is only a small constant.
The question is how much. Here are the values...

The amount of gas required to get my trailer up to 60 MPH.
60MPH is 26.8224 m/s
5000lb Trailer is 2267.962kg
Energy is 819462.2116 J = 8.2E5 J. (2267kg trailer going 26.8m/s)
Energy in 1 gal gas is 1.3E8 Joules
Energy Trailer used is 0.0063 GAL, 0.05 pints of gas, 0.8 oz
Engines are only about 25% effecient. The gas used is 4 times more.
0.0063 Gal x 4 = 0.0252 Gal, = 0.2 pints, 3.2 oz ounces.
3.2 oz gas to get a passive trailer up to 60 MPH.
(Counting engine and radiator heat; Not counting air friction along the way; Not counting transmission heat.)


Let us be fair: What if there is a lot more stop and go...
Two scenarios: Stop and go twice a minute. And, the other, one stop and go every hour. This should constitute a range of maximum possible to a minimum. I may be able to get the trailer up to 60 in 15 seconds and brake in 15 seconds. In other words, suck in gas and obtain a speed of 60MPH. Burn off that energy in the brakes and throw it away. Suck in more gas, and repeat the process. It is not a practical stunt because you will burn up a perfectly good transmission and 8 brake pads and some rotors.
But in the interest of academics, this will be my Maximum.
Maximum momentum consumption trailer is at 0.0252gal every 30 secs, applied continuously is 3.0 gal/hr
Minimum momentum consumption trailer is 0.0252 gal/hr, one stop and go per hour.
Everyone's driving habits will be somewhere in between. The energy of changing the momentum, as fast as mechanically possible, a stop and go every 30 seconds, still only has a gas consumption of 3.0 gal/hr;

Now for the truck...
If the truck weighs the same as the trailer, the energy in the changing momentum will be the same: Anywhere from 3 gal/hr to 0.0252 gal/hr. Average could be only a pint of gas.

And for both the truck and trailer, stop and go, could be two pints. A quart of gas for momentum changes, does not compare to 6 gallons steady state friction. Therefore, the weight of the truck does make a small difference in the purchase selection of a truck. But still, a trivial point because of the necessary weight of the trailer, and the small amount of gas used.

If we consider both truck and trailer, the maximum energy is 6 gal/hr, stop and go. This just happens to be the same energy of a steady sustained air friction at 60 MPH, 6 gal/hr. But it is not comprable. In a real world practical stop and go example would be way less. That is because only normally used trucks would exist; all other trucks have burned up transmissions and brakes. They are not real.
So, I am glad that I neglected the topic at first. Waste of time.



I am also going to neglect the topic of the energy of going up and down hills. This is the Force of Gravity times the vertical Distance. The reason is Regenerative Braking. Ford trucks already have this option. Dodge has made a feeble attempt. And several years ago, I dreamed of putting a motor/generator on one of my axils of my trailer. I will let someone with more money and time do it. In the future, trucks, cars, and trailers will have Regenerative Braking. And hills will not be as high. My point is that, in the future, the weight of the truck and trailer will be of less concern because of energy management.


In conclusion:
Any Gas truck, in the range of 18 to 24 mpg freeway, will have a 10 mpg pull economy for my trailer. And perhaps, the 24 is pie in the sky when towing. Their engine performance curves are sharper and more efficient, highly tunned and specialised. They are delicate, and can not hold torque and power under load. Even though adaptive tuning does help for towing, I do not think the 24 can be translated directly into the equation in a practical sense.
AT least that is my opinion...

However, a 30 mpg diesel can easily get 18 mpg pulling economy. Diesel has a higher fuel energy content, and diesels have consistent torque, and more of it.

My discussion only involves standard full size gas trucks. And my discussion only involves my trailer with its unique frontal area and mass. Nevertheless, the principals apply to all trucks and vans and to all trailers. Also, the discussion applies to all stupid sales people.

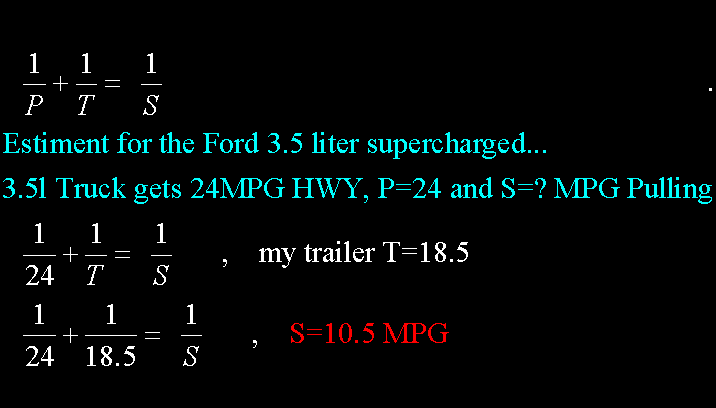
The fuel economy of the truck has little bearing on the overall pulling economy.

C.A.Pennock