SWR CONVERSION

index

SWR Conversion

Nonlinear Converters

Parameters such as power are not read directly as power, but only as a simple representative voltages: They are interpreted as power. And in the past, two methods have been used to read nonlinear representations.

The oldest method uses an analog meter, which has on its face, scale divisions that are painted unequal distances.

The face translates what a voltage actually represents. For remote applications, the problem is that you must have a selection of several of these remote analog meters, all with graduated face markings.

The second method employs electronic circuits to transform the linear voltage to a nonlinear voltage. The method uses amplifiers that shape the response. For example, Op amps can do this with staged diode feedback. Commercial converters are sold for $200 to $400 each. Broadcasters were required to spend this kind of money because the FCC required tracking accuracy and type acceptance.

But computers invite a third method which - by far - is the most accurate, versatile, and simple:
Conversion by software.

swrconv	proc	far	;convert swrw to
	push	bp
	mov	bp,sp

Conversion of VSWR for the broadcaster to a practical unit...

Transmission line

REFLECTOMETERS:
Measurements are made from "Heads", and "Inserts, or "Slugs". Inserts may have the diode inclosed in the sealed unit. Heads do not have diodes; they are expensive; and can also be used for spectral analysis. The rectification may be from vacuum tubes, like the 6AL5, or special "diode-circuits" with zero offsets. Heads and inserts can be rotated 180 degrees with calibrated snap-positions. Heads can be adjusted to varing depths; Each head has isometric voltage graphs printed on several pages of paper which are supplied by the manufacturer. Both have a small voltage output of approximately 100mV; not much more than what will drive a meter directly. In fact, inserts typically drive meters directly. Selected locations, located through out a broadcast plant, have mated pairs of inserts and meters; supplied by the manufacturer with matching serial numbers on meter and it's insert. Heads always are wired with schielded cable to special amplifiers; responsible for slight linearity corrections and amplification. Output voltage is several volts.

The calibration of the Reflected power is simple and straight-forward:
Turn the head, or insert, 180 degrees - opposite to it's normal operating position. The head will now read an "incident power". Calibrate this "incident" reading for 100% on external meters. Rotate the head back to normal position, and you will see the reflected power. It is CRITICAL that you realize that the procedure establishes a ratio, or percentage. The procedure does NOT establish the "VSWR". The "raw" returned voltage is absolutely necessary in my remote control work, and also in the transmitters logic. The vswr is derived later, and has no purpose that I have ever seen.

the problem: "wave-measure"

Vi= Voltage of the incident or forward wave.
Vr= Voltage of the reflected wave
SWRm= Standing Wave Ratio expressed in wave (minimum, maximum) measure.
The measurement involves minimums and maximums of a wave.
SWRm=(Vi+Vr) /(Vi-Vr) (from physics).
What is not obvious -from this simple equation - is the fact that this equation is part of a "wave equation." Wave-equations are useful in the science lab and in acoustics; they are not useful in transmitters.
Empirically, (in the field), it is convenient to obtain either Incident voltage or Reflected voltage.
In fact, the measurements are commonly gathered by REFLECTOMETERS: diodes placed in the transmission lines.

However, with such, the once simple readings are transformed into a "VSWR" (a wave measure) that no longer is intuitive.
Most transmitters have an electronic converter (computer, in fact) that reads out SWR in wave-measure (SWRm).
Older transmitters have an analog meter calibrated in wave-measure; Bad face, but the underling voltage is linear and good.
"Wave-measure" carries little useful information to an engineer. What an engineer - really - needs to know is how much power is being reflected, to determine if something will burn-up; or how much voltage is being reflected, to tell if transmission lines or components are going to break down and arc. With only wave-measure values, an engineer must rely on lookup tables, which are specific to particular transmission lines and foreward power.

graph of SWR=(1+R)/(1-R)
SWR ("Wave-measure")

X-axis is the ratio of reflected voltage to forward voltage. The X-axis is liniarly graduated in marks every 10%. Note that the ratio can never be greater than one (100%); or less than zero.
Y-axis is the SWR in "wave-measure". Note that it can never be less than one, and is always stated first with a "one" in front, such as "one point zero five". The graph is valid in green, and the graph in red is out of normal range. There are two asymtotes: one at x=100%, and one at y=-1.

The green line crosses the y-axis at one. This is a wave-measure swr of 1.00. Before you double that tiny distance to a value of 2 on the y-axis, the transmitter has already been shut down. A high power broadcast transmitter will shut down in between the values of 1.0 and 2.0; probably about 1.5. This is a very small operating range, and requires greater resolution and greater line slope. Greater resolution is not obtained untill about 80%. Unfortunately, this is not the normal operating range of transmitters. Wave-measure is not practical for transmitters.

Phrases, such as "1.05 SWR" or "1.01 SWR", use the "wave" vernacular. One must reluctantly concede that the nomenclature is well ingrained: For years, I have calibrated transmitters to begin "power-cut-back" at an SWR of 1.30: and a total transmitter shutdown at an SWR of 1.5 or greater. One must use the vernacular in order to set the transmitter.

A more practical unit would be the "power-ratio". Simple! Carries direct meaning; And everyone understands it intuitively. Also, Vi (Incident voltage) and Vr (Reflected voltage) are the easiest values to obtain directly (electrically) from a transmission line. And also, fortuitously, "power" and "reflected power" are common values associated with any transmitter. They are "natural" values returned directly from the source: RF power from transmission lines. Conversely, and, unfortunately, "Wave-measure" is a contrived measure, polluting the day-to-day measurements that are out in the "real world".

Neither can a control program work with wave-measure values: It will not - accurately - know what to do!
I, personally, as an engineer, could have tolerated the nomenclature, as countless other engineers have done for years. But, that was before I invented my control system! Now with VSWR in vogue, my system would have to digest it; and have to "deal" with it.

"It is the spirit and not the form of law that keeps justice alive."
- Earl Warren

There are times when a control engineer can not conveniently get to the desireable reflected VOLTAGE at the transmission line. In such a case, in 1993, my control program had to have a method to calculate the reflected power. No formulas are available. In 1993 I derived a formula of my own; a precise, analytical solution. A formula with the independent variable as the SWR, and the dependent variable as a ratio (or percentage). In other words, the Ratio-measure as a function of the SWR (wave-measure). The present equation needs to be flipped around - with the SWR on the right, and the Ratio on the left.

RULERMAR

Let PWRr=Reflected power
Let PWRi=Incident power or forward power
So that RW = PWRr/PWRi ( Ratio of watts. Later this equation will become SWR%).

SWRm=(Vi+Vr) /(Vi-Vr) ...Value always > 1
SWRm=(1+Vr/Vi) /(1-Vr/Vi) ...Algebraic manipulation.(Devide numerator and denominator by Vi)
Let RV = Voltage ratio = Vr/Vi ...Definition
RV = Vr/Vi
SWRm=(1+RV) /(1-RV) ...Substitution

EqnSWR1.gif, 1 kB

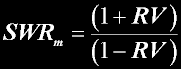RV is the voltage ratio.
SWRm is the Standing Wave Ratio.
This SWRm happens to be expressed in terms of voltage: or "VSWR", or "voltage standing wave ratio".

RV = Voltage ratio = (RW^.5) ... Sense P=E^2, (W=V^2 Watts proportional to voltage squared.)

SWRm=(1+(RW ^^.5) / (1-RW^^.5)

EqnSWR5.gif, 2 kB

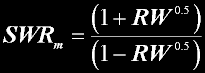Power (wattage) is easily treated by simply squaring the VOLTAGE reading.
(As long as 100% power is referenced to unity. Or if a ratio is expressed: cancelling the resistance. )
Squaring the voltage reading, in the computer software, will yield power.
The basic idea is P = V² / R
This simple equation works for resistors, or for resistive RF loads.

Desire Wattage Ratio...

But we want either SWR% (a percent) or RW (reflected watts): the original values obtained directly from the transmission line. .
This innocently looking formula is algebraically difficult to solve.

RULERMAR

SOLVING THE EQUATION...

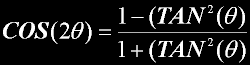
Equation from trig.

Here is help - a double-angle formula.
COS(2ø)=(1-(TANø)^²) / (1+(TANø)^²)

Note: Numerator and denominator are flipped;
But this form is otherwise the same as (1+X) / (1-X);
If we let X=(TANø)^2 .

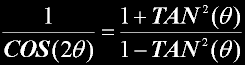
FLIP trigEquation

1/COS(2ø)=(1+(TANø)^²) / (1-(TANø)^²) ...flip

Assign SWRm : SWRm = 1/COS(2ø) ...define part1 of 2
Assign the left side (SWRm) to the left side of the trig equation (1/COS(2ø))

SWRm = 1/COS(2ø),
COS(2ø) = 1/SWRm
2ø = ACOS(1/SWRm)
Ø = (ACOS(1/SWRm)) /2

RV is a desired ratio (expressed in voltage): RV = (TANØ)^²
RV = (TANØ)^² ...define part2 or 2
Or, sense a power ratio is the square of a voltage ratio...
RW=RV^2 ...desired ratio
RW = ((TANØ)^^{2)^}2 = (TANø)^⁴.
It doesn't matter: either RW OR RV.
(RW is actually more direct since RW*100=SWR%)

Substituting part one into part two:
Ø = (ACOS(1/SWRm)) / 2 ... Reiterating Ø
Eliminating Ø ...
RV=(TAN(ACOS(1/SWRm))/2) ^² ...SWR ratio in volts.
We are not interested so much in volts, so lets get to power ratio.

RW=(TAN(ACOS(1/SWRm))/2) ^²^2 ...SWR ratio in pwr

RW=(TAN(ACOS(1/SWRm))/2) ^⁴
Standing-wave Power-Ratio is the Tangent to the forth power, of half of the Arccos angle of the wave-swr.

RW is, by our definition, a ratio of reflected to incident power:(SWR%, SWRrw). RV and RW are "standing-wave-ratios": one in voltage; one in power.
We now have a conversion formula to transform SWR in terms of waves (SWRm wave-measure), to SWR in terms of a power-ratio (SWRrw) or percent-power-ratio (SWR%).
The program code in a microprocessor, or the program code in a computer can now easily substitute the SRWm on the right side of the equation to yield the RV result on the left. If I could not have gotten this equation, there are other techniques: such as computer iteration approximations (such as Newtons), or perhaps code tables. Disgusting prospects! Because they are not "elegante". However, knowing something about computer writing, I would suspect that iterations would be faster. I will always choose a precise analytical solution to a faster numerical one. The matter is resolved by dignity and good personal taste. Above all else, my control system will have "appropriate" parameters. So there.
SWR%= 100*SWR_RW
RULERMAR

But we should test it.
...Let us suppose a value. If, for example, 5% of the power is being returned, SWR%=.05 then...
SWRm = (1+SWR%^.5) / (1-SWR%^.5)
SWRm = (1+.05^.5) / (1-.05^.5) ...substituting..05
SWRm =1.57601
Does our formula work?
SWR% = (TAN(ACOS(1/SWRm))/2) ^4
SWR% = (TAN(ACOS(1/1.57601))/2) ^4 ...substituting
SWR% = .05000 = 5%
RULERMAR

Why wasn't this equation developed before?

Because there was never a need to go back and forth, as is the case now. Just a press of the mouse, in my computer program, and one can choose which units they prefer. Only an intelligent, and user friendly control system - such as mine - would demand it. Can you imagen how cool this is? I am so hyped..."
CHICKENgif

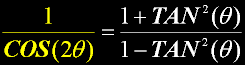
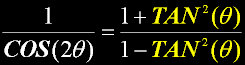
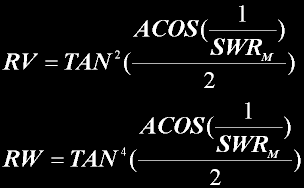
My conversion formula
RV=Ratio (in volts)

Don't look for this equation before March 1993. You will not find it. At least, I could not find it... The mathematical gymnastics yield an analytical solution that only involves a double-angle formula; something found in the trig section. Naturally, it is found here - because of it's inherent wave nature. If anyone ever names my equations, I wish for them to be called what they are: "SWR conversion" equations.

Here is a graph of the inverse function - inverse because the new Ratio-measure is a function of the old SWR-measure. The vertical axis now contains the 10 graduations of reflected power: 10%, 20%, 30%... on up to 99.9%. "100%" is asymtotic, as it will never be reached.
RULERBOWGIF