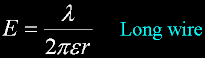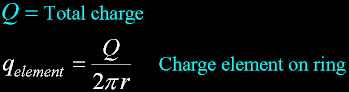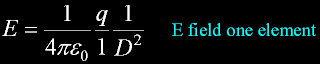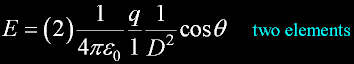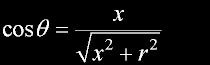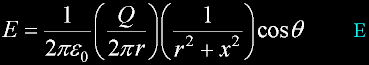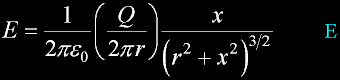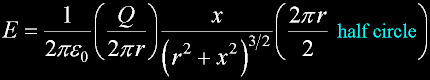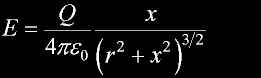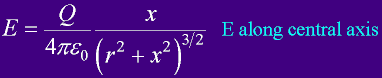

|
ELECTROSTATIC FIELDS |
|
ELECTROSTATIC FIELD
 Electrostatic Field
Electrostatic Field
|
 Field strength: Force/q ...Definition
Field strength: Force/q ...Definition
Fields can not be directly measured. But effects can be measured. Here is one: Force.
CGS System:
One dyne of force; produced by one statcoulomb to one statcoulomb charge; one cm away. ...Definition
SI System:
One Newton*4piEpsilon of force; produced by one coulomb to one coulomb charge; one meter separation.
Electrostatic fields - and All fields - are a measure of line density through an orthogonal surface space.
Total Flux, Gauses Law:
 Volt meters, N m2 C-1
Volt meters, N m2 C-1
Electric FLUX on any open surface
A is the surface that E is penetrating.
Electric FLUX on closed surface
A is the surface that E is penetrating.

 Gauss Law
Gauss Law
Total Electric Flux is the sum of all electric field E passing through all normal surface A.
Q is totally contained and continually described through any contained surface.
A totally contained surface is a CLOSED surface.
The total normal components of electric Flux through any closed surface is equal
to the charge inclosed by that surface. No matter how you package a Q, the flux is still
just Q coulombs.
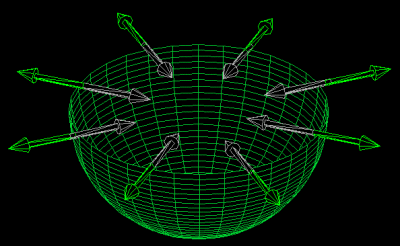
I should point out that inside a sphere the electrostatic field is zero. The electrostatic
field is a vector, and as such the net vector sum is zero.
Depected is positive charge. But negative charge works exactly the same way:
The charge distributes itself equaly on the shell, and there exists no charge field
anywhere inside the sphere - not near the walls nor at the center. (Mathematically,
gravity shows the same nulling inside a shell.)
I think I will write a page on spheres. It is that important.
I will need to anyway, when I talk about gravity.
 Anatomy of Spheres
Anatomy of Spheres
A vandergraph machine places charge on the top shell from the INSIDE of the top shell.

 Force
Force
This force was a defining equation at the beginning of electrostatics;
being something easily measured.
 Electrical Field strength E
Electrical Field strength E
 Maxwells first equation...
Maxwells first equation...
Known also as Gauss Law.
The surface area of a sphere is 4pir2.
Transpose the E to right hand side to obtain
Coulombs law...
The Electric Field strength in SI units
in any direction (vector)
Electric Field strength is also volts/meter
 Force
Force
The Force...
 Energy W, U
Energy W, U
The Potential Energy in SI units...
Joules
Path independent work
In-line work.
If charges are of opposite polarity, the final energy is negative, which is the stable, or low state.
(I will talk about entropy later.)
 Volt V
Volt V
Energy-Potential in J/C (Joules/qoulomb) around a single charge.
A special name for this J/C in an electrical field is the "Volt"
Voltage is energy/q, or electrical energy without its current.
I guess you could say "electric-potential" without
saying Potential-Energy.
Objects have voltage potentials. Here is a metal sphere of radius r.
Potential is measured in volts from one object to another.
It will have a density of this...
Notice, in the equation, that the charge distributes itself on the surface,
and does not depend on the volume. Somewhat intuitive; Also notice that the charge density is greatest around sharp points.
Arcing and corona will occur - if all else is equal - at smallest curvature.

 Two parallel plates each of area A separated by distance d in air.
Two parallel plates each of area A separated by distance d in air.
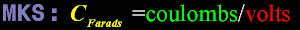
I made this "capacitor" out of two CDs. And now that you know, you will recognise it.
You will have to assume the surface is conductive. I did the hard part.
Charge in a uniform field in terms of uniform density...
A is total area.
A capacitor...
A special case: a uniform electric field.
Place a total charge Q on one plate. Then either plate will have 1/2 the charge (as a system).
The charge will distribute itself.
(A is now understood as the area of just one plate separately.)
Now we leave the surface of the plates and look at the energy U between the plates...
And, the same as in the case of a point charge; we take the product (in this case scaler) of the field and the distance
across the plates that a charge would travel in doing work.
Electric Field in terms of Density
Substituting density to eliminate density
Electrical Potential Energy of two plates containing Q.
Energy in terms of Electrostatic Field strength between the plates.
We see the energy is proportional to the square of the field E.
 Field Energy
Field Energy
And in general...
And not just for a CAP...
(The general equation can be derived without using a capacitor.)
Now that we are dealing with a capacitor, observe the geometrical term volume. We can derive the capacitor dimensions and
the definition of a capacitor (with one additional term, the dialectic).
 Define a capacitor in terms of charge and voltage.
Define a capacitor in terms of charge and voltage.
The voltage is this...
Where each plate has a charge density p.
And l is the distance of separation.
 Define a standard capacitor in terms of purely physical dimensions.
Define a standard capacitor in terms of purely physical dimensions.
Define capacitance in terms of geometry.
The capacitance value has a special name: Farad.
or this...
add in a dialectic...
Various types of physical material can be added in between the plates.
The dialectic constant must be added. This constant is by definition simply
a scaler that is a multiplier and can be simply added.
 Field Energy
Field Energy
The energy of a cap expressed in terms of voltage and capacitance.
As the q travels across - the voltage changes. Therefore an integral is needed.
The voltage of charge on a sphere.
Large amounts of energy can be stored in a dielectric.
In this equation the dielectric
is air, but for different substances such as glass (I think) the dielectric is five times larger. In this case, if the energy is established
with a certain dielectric, and you then remove the dielectric and place it over in a corner, you have removed 4/5 the system
potential energy. You may regain some of the energy by replacing the dielectric. Most of the energy is in the dielectric.
 Field energy density
Field energy density
J/m3
Joules/cubic meter
As the separation increases - with established q not changing - the VOLTAGE goes up as measured between the two plates.
(As the separation distance increases further, the two disks behave more and more like point charges, and the
disk surface becomes less of a factor.
That is to say, the area remains proportionally much larger than separation distance. A >> d.)
The action of the capacitor is to reduce voltage, either by proximity of the
plates;
or from a good dielectric.
This is the definition of a capacitor: c=q/v. And it translates to more of a physical definition than anything else.
As separation distance goes up, then capacitor action goes down, and - necessarily - voltage goes up.
A "great" capacitor holds a lot of qoulombs at low voltage. It has a lot of surface area, small separation, and high
dielectric constant.
In broadcast work, one aspect of plate separation is called "loading". When tuning controls increase the separation
distance, the loading is decreased, and HV potentials will increase between the capacitor plates as well
as other circuits. The results can be catastrophic
failure for insulators and tubes.
This is a dynamic effect of RF potential,
but the corollary to static charges on simple plates is exactly the
same effect. I have been personally involved with this effect for over 35 years,
involving countless adjustments.

 I have discussed aspects of current in terms of electrostatics. But there are magnetic aspects as well.
I have another page for magnetics. And yet another page after the two (magnetics and electrostatics) are combined.
Perhaps I need a transition page, as the two can not really be seperated.
I have discussed aspects of current in terms of electrostatics. But there are magnetic aspects as well.
I have another page for magnetics. And yet another page after the two (magnetics and electrostatics) are combined.
Perhaps I need a transition page, as the two can not really be seperated.
 Displacement Current
Displacement Current
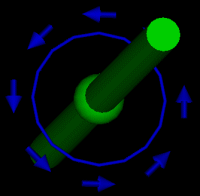
Conventional Current
|
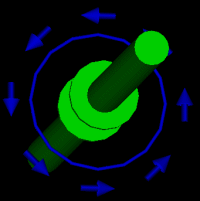
Displacement Current
|
dL line in blue
B arrows in blue
current in green
Displacement Current
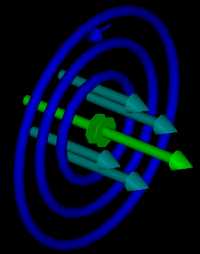
Maxwell defined the current in a capacitor: "Displacement-Current".
Here is Maxwells fourth equation. Consider only the second term...
What is not specifically a moving charge is a changing electric field in general.
The two concepts are exactly the same mathematically.
When I talk about magnetic fields this Maxwell contribution will become very important.
This equation will power all transformers and solenoids; and in fact, led Maxwell to
predict and describe electromagnetic radiation as a wave.
A disk capacitor of radius r:
The area orthoganal to the electric field in the capacitor.
This "invisible" current is equal to the rate of change of the quantity of coulombs charge
on the plates.

Conventional Current
|
Displacement Current
|
the Complete Ampere
The complete total current...
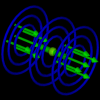 This leads to Maxwells fourth equation, and a more complete Amperes Law...
This leads to Maxwells fourth equation, and a more complete Amperes Law...

 Maxwell-4
Maxwell-4

 I want to consider a couple of special geometries of electrostatics:
I want to consider a couple of special geometries of electrostatics:
an infinitly long wire, and a ring...
The force of an electrostatic charge was defined in terms of a point charge.
However, the current (amp) was defined as force from a long wire.
An infinitly long wire...
An infinitely long wire...
By substituting a density value of one coulomb per meter in the wire at a distance of
one meter, then one sees that a definition using a wire would be twice as strong as one
using the established point charge. Interesting...
 A Ring
A Ring
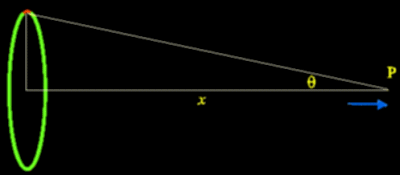
A ring of equal distribution of total Charge Q.
Diagramed as a positive charge by the blue arrow pointing outward.
Ring Radius of r.
Distance away from ring is x.
The actual E line
from an infinitesimal element
is the diagonal...
General E
For a ring with one element.
Balance a second element on the opposite side of the ring.
The E component toward the center of the ring will be this...
Using symmetry, I have eliminated vector algebra.
Substitute D diagonal and Replace coso...
Integrate for a half circle around the loop...
Electric field along central axis...
In contrast to a B field, this E field has a maximum some distance away from the loop.
A B field is at max in plane of loop, directly in center of loop.
 This is because the defining
criteria is one of "force", which, for both fields, is a vector. I assert that all fields
can not be directly measured, and as such, in fact are scalers. Force is only one small property of
a field because it is a vector. (This notion is a personal conjecture.)
This is because the defining
criteria is one of "force", which, for both fields, is a vector. I assert that all fields
can not be directly measured, and as such, in fact are scalers. Force is only one small property of
a field because it is a vector. (This notion is a personal conjecture.)
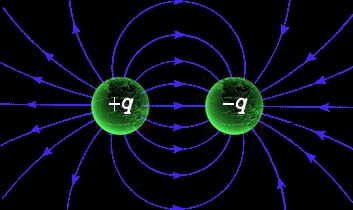
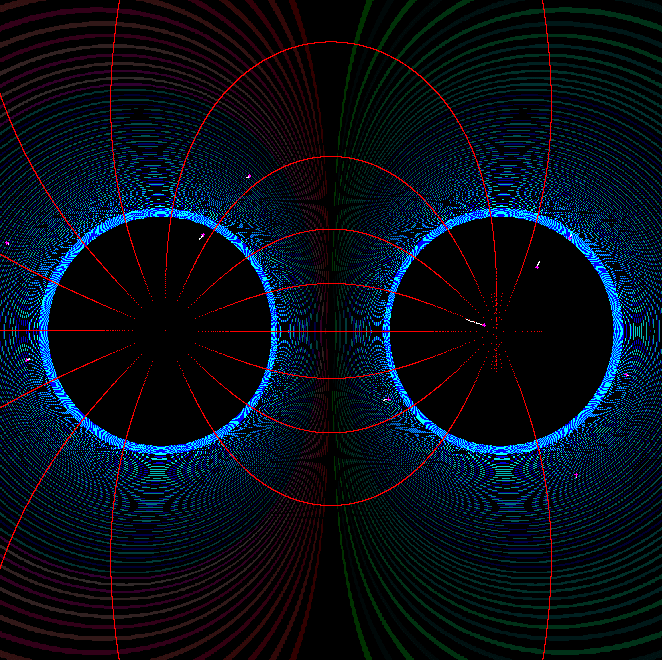
Here is my computer generated graph of either two unlike point monopole charges or
two point magnetic co-poles. North pole on the left or positive charge on the left.
The countour lines in cyan are absolute magnitude or vector-length or electric E or magnetic B.
The lines in red are
vector direction lines or "force-lines". These are the lines conventionaly drawn.
But what is generally ignored are the contour lines indicating absolute value.
They are scalers.
In the center of each charge, the value goes to infinity, and I have left it black indicating
that the area is undefined. In between the charges, the value goes to zerro (for unlike charges).
A unit vector goes to infinity here and is likewise undefined.


 Electrostatic Field
Electrostatic Field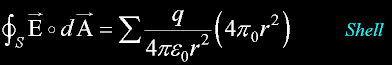



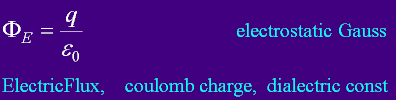
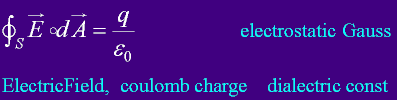
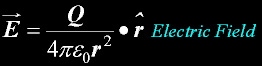
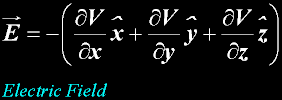
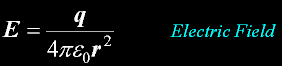
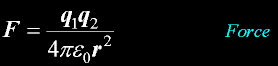
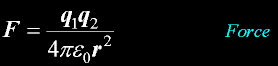
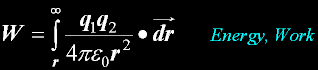
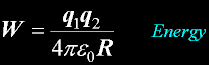
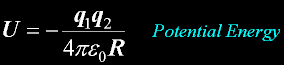
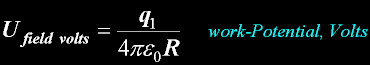
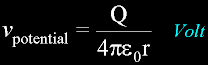

 Two parallel plates each of area A separated by distance d in air.
Two parallel plates each of area A separated by distance d in air.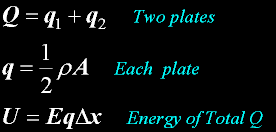
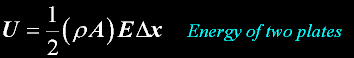

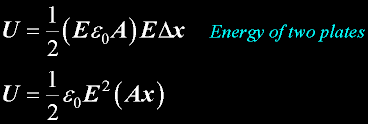
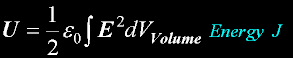
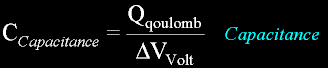

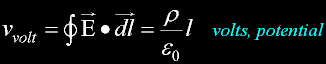
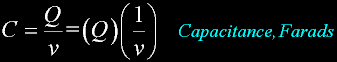
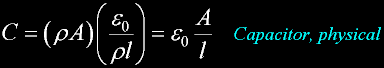
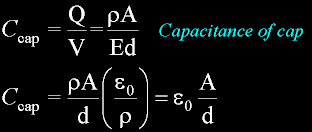
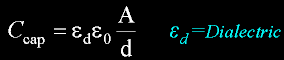
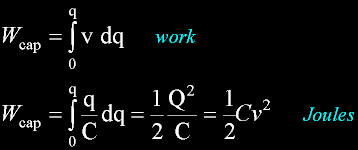
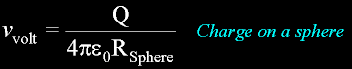

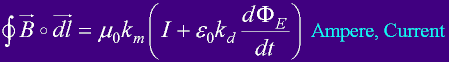
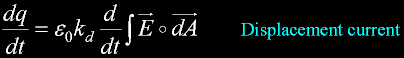
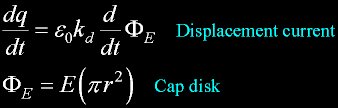

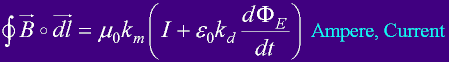
![]()
Maxwell-4