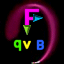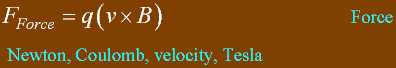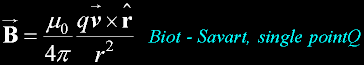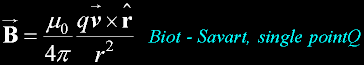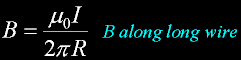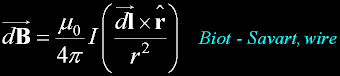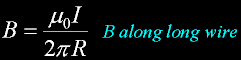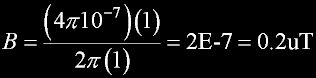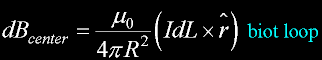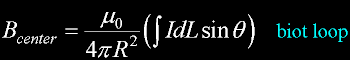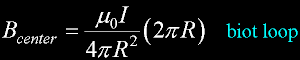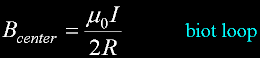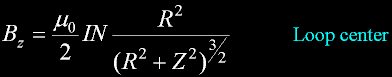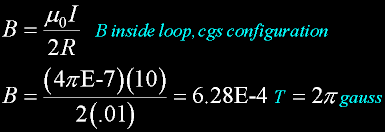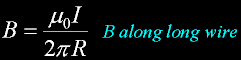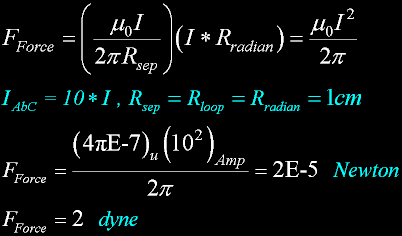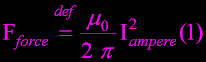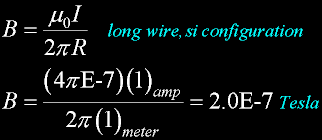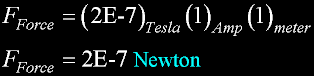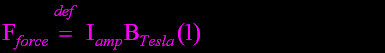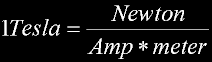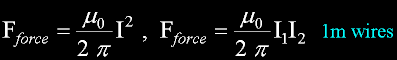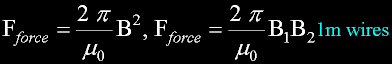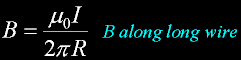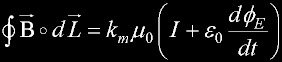Magnetic Fields

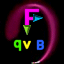
Lorentz Magnetic force F
SI units:
Force (Newton) from a Magnetic field B in Tesla.
Charge q is Coulombs, and v is velocity m/s.


Biot-Savart B point charge
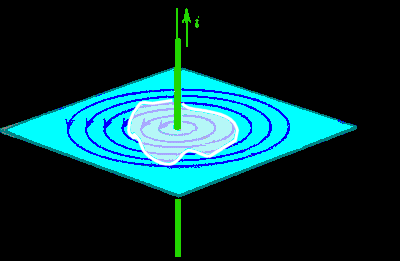
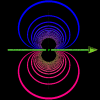
Contour of magnetic density (orthoganal to field lines) of a moving point charge.
Showing intensity - not direction.
The direction is toward the observer on top (blue, and into page on the bottom (red).
dB because the current element is moving.
dB is in Teslas
dz is the axial infitizimal distance from element.
I is Amps.


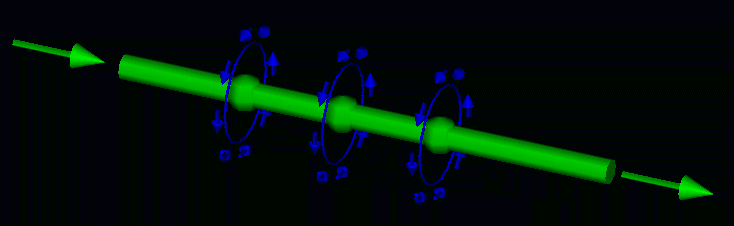
From a discrete free point coulomb particle - to discrete drift current carriers in a wire...
Biot-Savart B wire-current

I have derived this equation in full, from a point charges, on another page.

I have derived this long straight wire current on another page.
Quantitively, it comes out perfectly.



A point in space near a steadily conducting wire.
Using Biot-Savart-amperes law eliminates the need to derive the current of a long straight wire.

With the condition that the B is per meter length. Length is cancelled.

The field of ONE wire carring one amp at one meter. 200 nanaT




Biot-Savart B Current loop
Current loop or magnetic moment
current loop - positive current in green.
Magnetic moment is the loop current times the inclosed area of the loop.


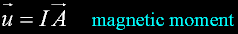
Every magnetic field line is continuous and connected (unbroken).

Simple case of a circle of radius R (Amperes law).
These two geometric configurations were used to define the ampere and the abampere respectively. (Abampere is equal to 10 amperes)

One abampere in a A wire loop of one cm radius produces One dyne of force to another similar loop.

This magnetic field strength density was defined as from one radian portion of the loop (one cm) as one gauss; or, for the whole loop circumference, as 2pi gauss (inside the loop).
So we go from force; to current; to a measure of a magnetic field B.


In general, a point inside the plane of a current "loop"...
A simple case: Current loop circumference is 2piR.
And substituting this simple loop...
We obtain this...

And here is the B out from the loop along the z azis. With z=0, it is the same equation.

Example...

One abampere in a a wire loop of one cm radius produces One dyne of force, per radian, to another similar loop.
That is to say: 2pi dyne for the intire loop.
The abampere is defined as the current that flows in a circle of one centimeter diameter and produces, at the center of this circle, a magnetic intensity of one oersted.
One Oe=79.6 amp/meter. But this statement declares nothing...
(or later restated...
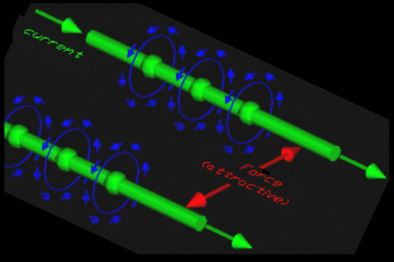
Two wires one centimetre apart carrying 1 e.m.u. of current (abampere) experience a force of two dynes for each centimetre of their length. )
I use this "defining-case"...
Because in the beginning of magnetics the cgs system was used. And they choose the loop instead of the long wire. This was restated to the long wire in 1881 and 1946. (But I will show both systems.)

The choice of the loop was premature. There is sevier magnetic line "leakage" between the loops. However, at the time, the physical configuration lint itself well to multiplying the current by wrapping hundreds of loops. The oersted and amp-turn are redundant and elude the problem by overstating the obvious. Computational computer iteration is a solution method by using Biot-Savart summation of infintisamal point currents. Torque (AxI) concept will be the best analytical aproximation.
Here is the magnetic field at the center of the loop.
2pi gauss.
(Same numerical value for the force of the intire loop area:
2pi dynes)


And here is the force...

First, the magnetic field B, one cm from the loop - as if it were a straight wire, out at the edge of the loop.


oops, I seem to have made a mistake...
that should be one dyne...


Amperes Law B
Amperes Law (infinitely long wire)
Measurement loop (in white) circumference is 2piR.

A trivial case (non vector) is B in line with dL at a radius R.
Resulting in amperes law near a long wire.
Aprox 1946, the ampere was defined...

"One ampere is that unvarying current which, if present in each of two parallel conductors of infinite length and one meter apart in empty space, causes each conductor to experience a force of exactly 2* 10^(-7)newton per meter of length."



The definition, coincidently, yielded the magnetic field indirectly.



Notice the same numerical value for Teslas and Newtons.)
Here is why...

Here is the force, with the given B...
2E-7 Newtons
from a magnetic field B (from one of the wires)
and from a current of one amp from the other wire.
(Same thing)

This equation is Defined this way. It comes without precedent. Here is a starting point in equation development. This MACROSCOPIC definetion gives no concern to what microscopically is actually causing the force, such as the Lorenz q motion equation.

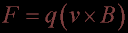
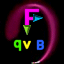
Both equations are totally equivalent, and as I have shown, one is derived from the other.


And, since the Amp is defined,
The Tesla is defined.
This definition uses a very much stronger stand alone magnetic field...

"A magnetic field of one Tesla is such that One Amp flowing in a wire of length one meter produces a force of on Newton."

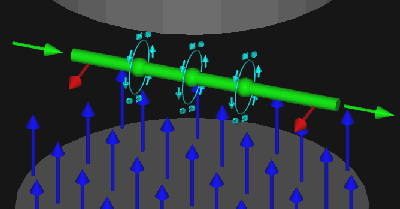
Force indicated in red.
All definitions from F=qvB. Migrating to F=ilB.
("The Lorentz Force")


There are three varieties of this equation:
F=IB F=II F=BB
You can navigate between them all with algebra.

The last of these equations is the most important in an analytical sense. Unfortunately, it is the one equation NEVER published in any text book or classroom. But it alone, epitomizes the true essence of force: force is only experienced between lines. Particles do not exist, and fields DO.
"Force" is an expression between field lines.
Tesla units = Newton/Amp-meter
u units =Newton/Amp2
F=B2/u= N2/Amp meter /N amp2 = Newton amp/meter




Local B in space near a steadily conducting infinite wire.
Biot-Savart B from equation above
Substitute B
Amperes Law B of long wire inclosing current by a path (surface). Open surface can be attached to this path-loop.
Path does not have to be a circle:
- any inclosed path that is penetrated by the current.
- any open-surface, defined as open at the loop, that is penetrated by current.

Amperes law involves currents through a surface...
And the two Biot-Savart laws above can be derived almost "onsight". Amperes law is convenient for many applications such as solenoids.

Solenoids:
The magnetic field within a loop of wire is not uniform. One the other hand, millions of tiny circular currents in a homogeneous substance produce a uniform magnetic field. By placing an iron core substance of high permittivity inside many loops, an efficient and strong magnetic field can be produced. Sympathetic induction from an outside loop(s) disperse one driven current to many internal magnets. Solenoids are a major technical application of magnetic fields.

This leads to a modification to Maxwells fourth equation. The physical material used in solenoids, transformers, and inductors will have a permitivity.

k is the relative permittivity: It can be diamagnetic, paramagnetic, or ferromagnetic.




Adding all the magnetic field lines through a surface...
Webers
Total magnetic flux on any open surface
A is the surface that B is penetrating.
This concept will become important when I combine Electrostatics and Magnetics in the next section.